COMPUTING THE VOLUME OF A SOLID OF REVOLUTION USING THE DISC METHOD
The following problems will use the Disc Method to find the Volume of a Solid of Revolution. We start with a region $R$ in the $xy$-plane, which we "spin" around the $x$-axis to create a Solid of Revolution. We then integrate the Circular Cross-Sectional Area of a slice of this solid taken perpendicular to the $x$-axis. This process is called the Disc Method. The Disc Method is a special case of Volume Using Cross-Sectional Area, which can be found
here . The details of the Disc Method are posted below.
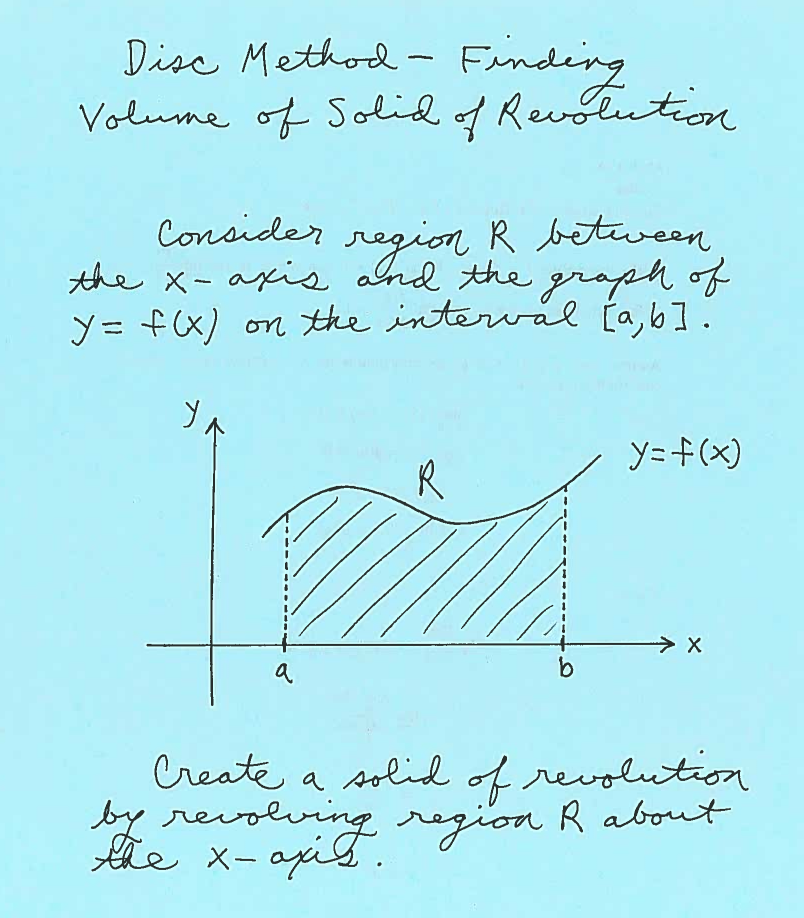
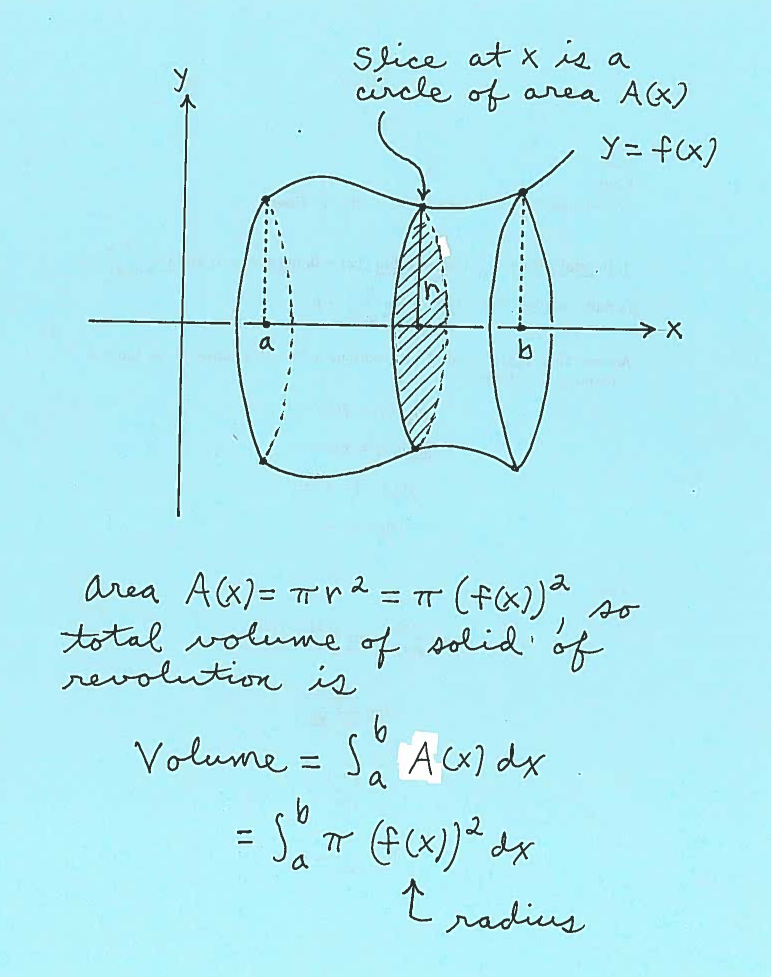
After reading the description of region $R$, we will SKETCH and CAREFULLY LABEL this region $R$. After sketching or imagining the resulting Solid of Revolution about a given axis, it will be our job to create a formula for the Area of a Circular Cross-Section of this solid taken perpendicular to the $x$-axis at $x$. This circular Area $ A(x)$ will depend on its radius $r$, which will be CAREFULLY MARKED in region $R$. This is a crucial step in the Disc Method process and is very important ! Then the Volume of the Solid of Revolution will be
$$ Volume = \int_{a}^{b} A(x) \ dx = \int_{a}^{b} \pi r^2 \ dx $$
We will eventually generalize the Disc Method by revolving regions $R$ about various horizontal and vertical lines, not just the $x$-axis.
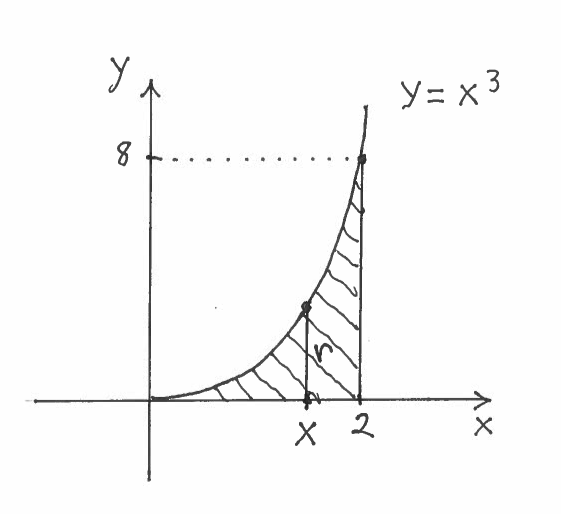
EXAMPLE 1: Consider the region bounded by the graphs of $ y=x^3 $, $ y=0 $, and $ x=2 $. Use the Disc Method (SET UP ONLY) to find the Volume of the Solid formed by revolving this region about
$ \ \ \ $ a.) the $x$-axis.
$ \ \ \ $ b.) the $y$-axis.
Solution a.): Here are a carefully labeled sketch of region $R$, a rough sketch of the resulting Solid of Revolution (a thumb tack ?), and a circular cross-section at $x$ of radius $r$. It is IMPORTANT to mark BOTH $x$ and $r$ in the sketch of the region !!!
 $ \ \ \ $
$ \ \ \ $
 $ \ \ \ $
$ \ \ \ $
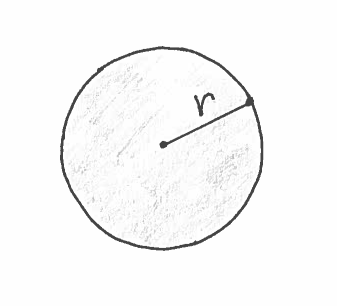
The area of the circular cross-section is
$$ A(x)= \pi r^2 = \pi (x^3)^2 $$
Thus the total volume of this Solid of Revolution is
$$ Volume = \int_{0}^{2} \pi (x^3)^2 \ dx $$
Solution b.): IMPORTANT CHANGE: Because we are revolving the region about the $y$-axis, we must make slices perpendicular to the $y$-axis at $y$ !!! This ensures that the slices are CIRCULAR. Here are a carefully labeled sketch of the region, a rough sketch of the resulting Solid of Revolution (a water bowl ?), and a circular cross-section at $y$. In this example, the cross section is called an annulus, a circular region of radius $R$ with a smaller concentric circular region of radius $r$ removed. It is IMPORTANT to mark ALL of $y$, $r$, and $R$ in the sketch of the region !!!
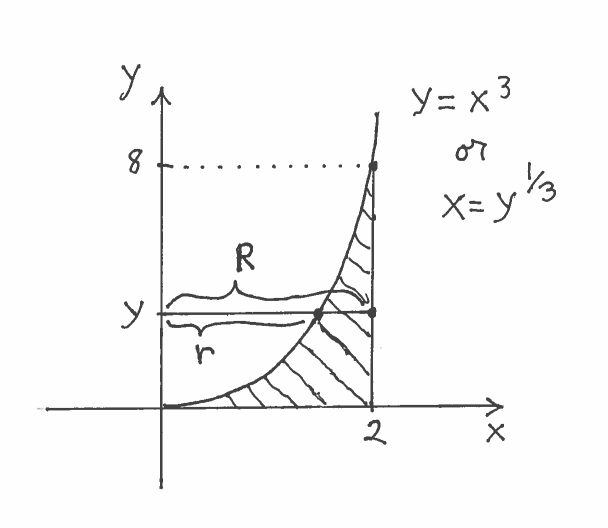 $ \ \ \ $
$ \ \ \ $
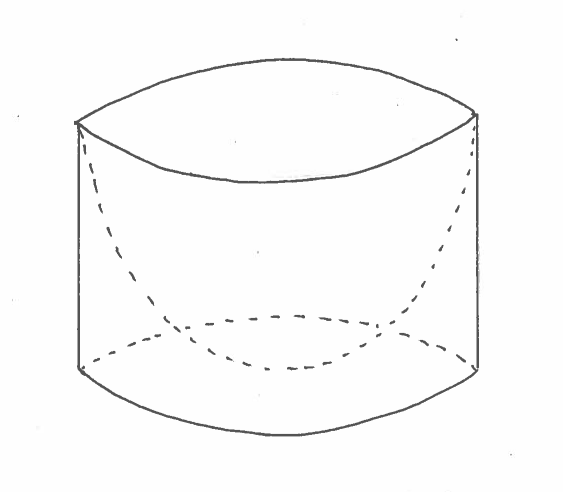 $ \ \ \ $
$ \ \ \ $
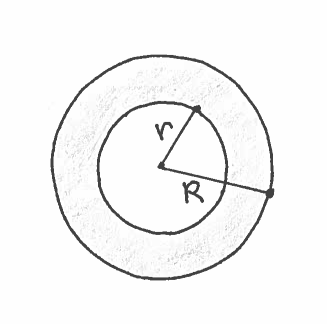
The area of the circular cross-section is now a FUNCTION OF Y !!! The area of this circular cross-section is
$$ A(y)= \pi R^2 -\pi r^2 = \pi (2)^2 - \pi (y^{1/3})^2 $$
Thus the total volume of this Solid of Revolution is
$$ Volume = \int_{0}^{8} \Big( \pi (2)^2 - \pi (y^{1/3})^2 \Big) \ dy $$
The following problems use the Disc Method to find the Volume of Solids of Revolution. Most are average. A few are somewhat challenging. All solutions SET UP the integrals but do not evaluate them. We leave the actual integration of the integrals up to you, using antiderivatives or online integrators.
- PROBLEM 1 : Consider the region bounded by the graphs of $ y=\ln x $, $ y=0 $, and $ x=e $. Use the Disc Method (SET UP ONLY) to find the Volume of the Solid formed by revolving this region about
$ \ \ \ \ $ a.) the $x$-axis
$ \ \ \ \ $ b.) the line $y=-1$.
$ \ \ \ \ $ c.) the line $ y=3 $.
Click HERE to see a detailed solution to problem 1.
- PROBLEM 2 : Consider the region bounded by the graphs of $ 2x+3y=6 $, $ y=0 $, and $ x=0 $. Use the Disc Method (SET UP ONLY) to find the Volume of the Solid formed by revolving this region about
$ \ \ \ \ $ a.) the $y$-axis
$ \ \ \ \ $ b.) the line $x=-2$.
$ \ \ \ \ $ c.) the line $ x=4 $.
Click HERE to see a detailed solution to problem 2.
- PROBLEM 3 : Consider the region bounded by the graphs of $ y=e^x $, $ y=1 $, and $ x=\ln 3 $. Use the Disc Method (SET UP ONLY) to find the Volume of the Solid formed by revolving this region about
$ \ \ \ \ $ a.) the $x$-axis.
$ \ \ \ \ $ b.) the line $y$-axis.
$ \ \ \ \ $ c.) the line $ x=4 $.
$ \ \ \ \ $ d.) the line $y=1$.
$ \ \ \ \ $ e.) the line $x=-3$.
$ \ \ \ \ $ f.) the line $ y=3 $.
Click HERE to see a detailed solution to problem 3.
- PROBLEM 4 : Consider a right circular cone of height $h$ and base radius $b$. Use the Disc Method to formulate the Volume for this cone.
Click HERE to see a detailed solution to problem 4.
- PROBLEM 5 : Consider a sphere of radius $b$. Use the Disc Method to formulate the Volume for this sphere.
Click HERE to see a detailed solution to problem 5.
Click HERE to return to the original list of various types of calculus problems.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by
clicking on the following address :
kouba@math.ucdavis.edu
A heartfelt "Thank you" goes to The MathJax Consortium and the online Desmos Grapher for making the construction of graphs and this webpage fun and easy.
Duane Kouba ...
October 7, 2020



 $ \ \ \ $
$ \ \ \ $
 $ \ \ \ $
$ \ \ \ $

 $ \ \ \ $
$ \ \ \ $
 $ \ \ \ $
$ \ \ \ $
