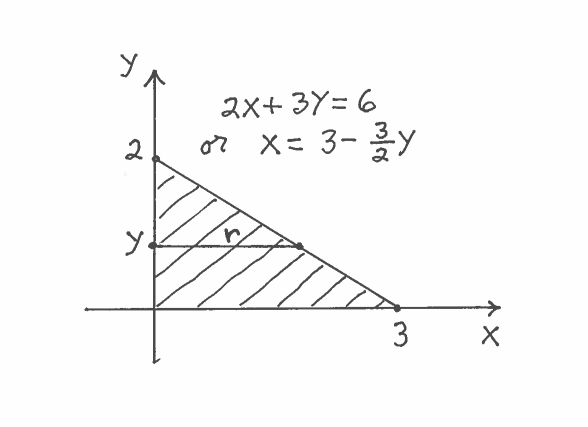
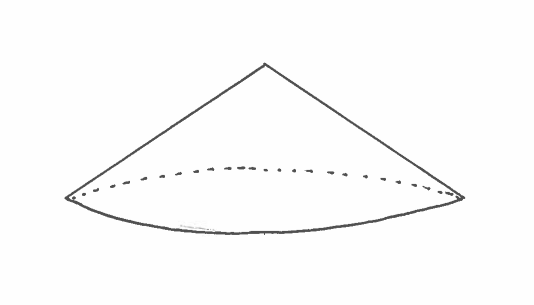
SOLUTION 2: a.) IMPORTANT CHANGE: Because we are revolving the region about the $y$-axis, we must make slices perpendicular to the $y$-axis at $y$ !!! This ensures that the slices are CIRCULAR. Here are a carefully labeled sketch of the region, a rough sketch of the resulting Solid of Revolution, and a circular cross-section at $y$. In this example, the cross section is called an annulus, a circular region of radius $R$ with a smaller concentric circular region of radius $r$ removed. It is IMPORTANT to mark ALL of $y$, $r$, and $R$ in the sketch of the region !!!
 $ \ \ \ $
$ \ \ \ $
 $ \ \ \ $
$ \ \ \ $
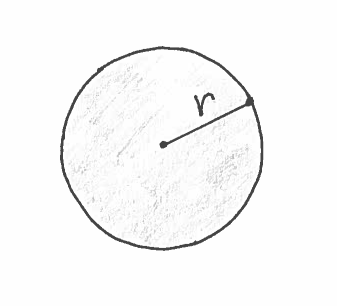
The area of the circular cross-section is
$$ A(y)= \pi r^2 = \pi (3- {3 \over 2}y)^2 $$
Thus the total volume of this Solid of Revolution is
$$ Volume = \int_{0}^{2} \pi (3- {3 \over 2}y)^2 \ dy $$
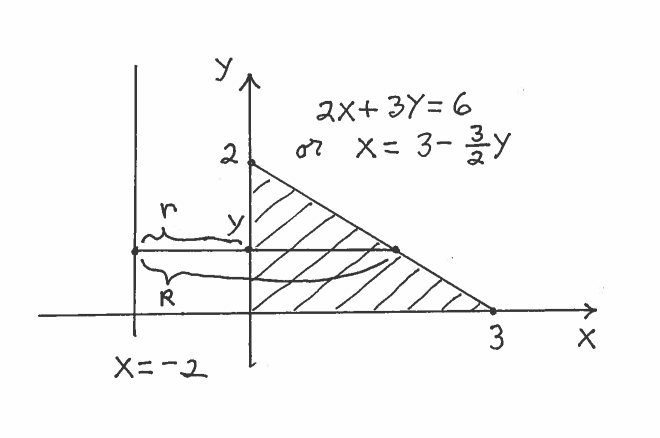
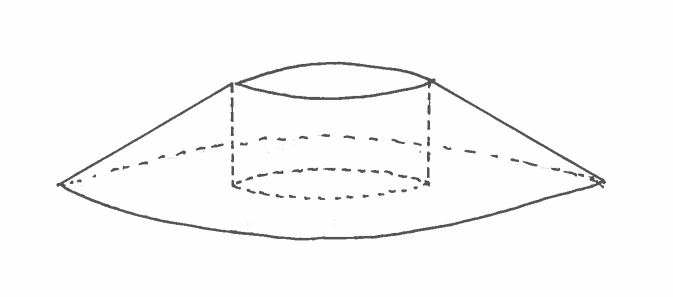
SOLUTION 2: b.) Here are a carefully labeled sketch of the region, a rough sketch of the resulting Solid of Revolution, and a circular cross-section at $x$. In this example, the cross section is called an annulus, a circular region of radius $R$ with a smaller concentric circular region of radius $r$ removed. It is IMPORTANT to mark ALL of $x$, $r$, and $R$ in the sketch of the region !!!
 $ \ \ \ $
$ \ \ \ $
 $ \ \ \ $
$ \ \ \ $
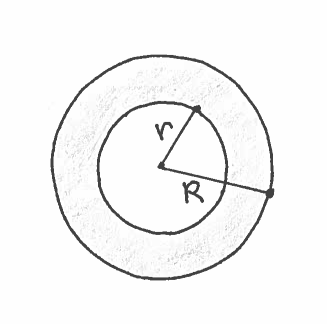
The area of the circular cross-section is
$$ A(y)= \pi R^2 -\pi r^2 = \pi ((3- {3 \over 2}y)- (-2))^2 - \pi (2)^2 = \pi (5 - {3 \over 2}y)^2 - \pi (2)^2 $$
Thus the total volume of this Solid of Revolution is
$$ Volume = \int_{0}^{2} \Big( \pi (5 - {3 \over 2}y)^2 - \pi (2)^2 \Big) \ dy $$
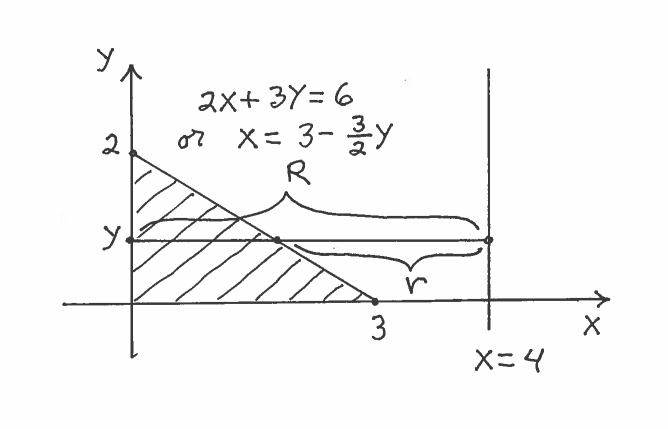
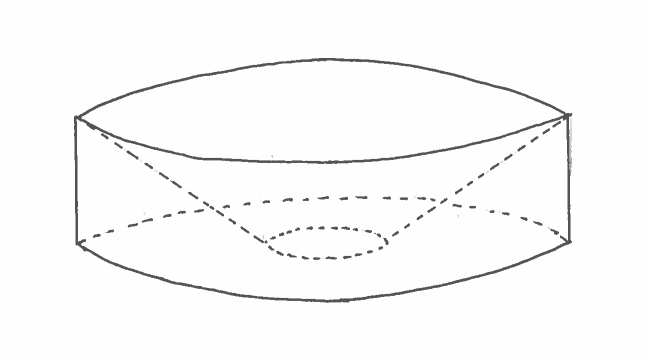
SOLUTION 2: c.) Here are a carefully labeled sketch of the region, a rough sketch of the resulting Solid of Revolution, and a circular cross-section at $x$. In this example, the cross section is called an annulus, a circular region of radius $R$ with a smaller concentric circular region of radius $r$ removed. It is IMPORTANT to mark ALL of $x$, $r$, and $R$ in the sketch of the region !!!
 $ \ \ \ $
$ \ \ \ $
 $ \ \ \ $
$ \ \ \ $

The area of the circular cross-section is
$$ A(x)= \pi R^2 -\pi r^2 = \pi (4)^2 - \pi (4- (3-{3 \over 2}y)^2 = \pi (4)^2 - \pi (1+{3 \over 2}y)^2 $$
Thus the total volume of this Solid of Revolution is
$$ Volume = \int_{0}^{2} \Big( \pi (4)^2 - \pi (1+{3 \over 2}y)^2 \Big) \ dy $$
Click HERE to return to the list of problems.
 $ \ \ \ $
$ \ \ \ $
 $ \ \ \ $
$ \ \ \ $

 $ \ \ \ $
$ \ \ \ $
 $ \ \ \ $
$ \ \ \ $

 $ \ \ \ $
$ \ \ \ $
 $ \ \ \ $
$ \ \ \ $

 $ \ \ \ $
$ \ \ \ $
 $ \ \ \ $
$ \ \ \ $
