![]()
so that we can now say that a partial fractions decomposition for
![]() is
is
![]() .
.
This concept can also be used with functions of ![]() . For example,
. For example,
![]()
![]()
![]()
![]()
so that we can now say that a partial fractions decomposition for
![]() is
is
![]() .
.
Of course, what we would like to be able to do is find a partial fractions decomposition for a given function. For example, what would be a partial fractions decomposition for
![]() ? Begin by factoring the denominator, getting
? Begin by factoring the denominator, getting
![]() .
.
Now ASSUME that there are constants ![]() and
and ![]() so that
so that
( equation (*) )
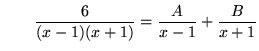 .
.
It can be shown that such constants always exist for the rational function
![]() if the following two conditions are met. They are
if the following two conditions are met. They are
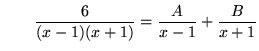
(Get a common denominator and add the fractions.)
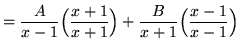
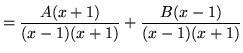
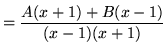 ,
,
that is,
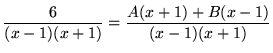 .
.
Since the fractions in the above equation have the same denominators, it follows that their numerators must be equal. Thus,
( equation (**) )
![]() .
.
The right-hand side of this equation can be considered a function of ![]() which is equal to 6 for all values of
which is equal to 6 for all values of ![]() . In particular, it must also be true for specific values of
. In particular, it must also be true for specific values of ![]() . For example, if we choose to
. For example, if we choose to
let ![]() ,
,
then
![]()
so that
![]() .
.
If we choose to
let ![]() ,
,
then
![]()
so that
![]() .
.
We can now say that a partial fractions decomposition for
![]() is
is
![]() .
.
It should be noted that ![]() and
and ![]() were chosen for use in equation (**) for their convenience of ``zeroing out" terms in the equation. However, any other two choices for
were chosen for use in equation (**) for their convenience of ``zeroing out" terms in the equation. However, any other two choices for ![]() will lead to the exact same values for
will lead to the exact same values for ![]() and
and ![]() (after solving two equations with two unknowns). Try it. After getting familiar with this process, in order to save some time, get in the habit of going from the step at equation (*) directly to the step at equation (**). Here is another important point to consider when applying the method of partial fractions to the rational function
(after solving two equations with two unknowns). Try it. After getting familiar with this process, in order to save some time, get in the habit of going from the step at equation (*) directly to the step at equation (**). Here is another important point to consider when applying the method of partial fractions to the rational function
![]() . If the degree (highest power) of
. If the degree (highest power) of ![]() is equal to or greater than the degree of
is equal to or greater than the degree of ![]() , then you must use polynomial division in order to rewrite the given rational function as the sum of a polynomial and a new rational function satisfying condition 2 above. For example, polynomial division leads to
, then you must use polynomial division in order to rewrite the given rational function as the sum of a polynomial and a new rational function satisfying condition 2 above. For example, polynomial division leads to
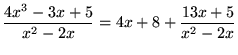 ,
,
where the rational function on the right-hand side of the equation satisfies condition 2. There are other points to consider. Recall that the complex number
![]() so that
so that
![]() and
and ![]() . In addition, if two complex numbers are equal, then their real and complex components are equal. That is, if
. In addition, if two complex numbers are equal, then their real and complex components are equal. That is, if
![]() ,
,
then
![]() and
and ![]() .
.
Now let's do another example. Find a partial fractions decomposition for
![]() . Begin by factoring the denominator, getting
. Begin by factoring the denominator, getting
![]() .
.
Now ASSUME that there are constants ![]() and
and ![]() so that
so that
( equation (*) )
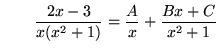 .
.
Since ![]() is an irreducible quadratic expression, assuming only that
is an irreducible quadratic expression, assuming only that
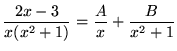
is NOT GENERAL ENOUGH and will not always lead to a correct partial fractions decomposition. Continuing, we have
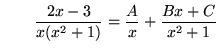
(Get a common denominator and add the fractions.)
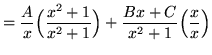
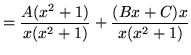
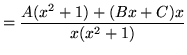 ,
,
that is,
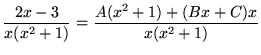 .
.
Since the fractions in the above equation have the same denominators, it follows that their numerators must be equal. Thus,
( equation (**) )
![]() .
.
This equation can be considered two functions of ![]() which are equal to each other for all values of
which are equal to each other for all values of ![]() . In particular, it must also be true for specific values of
. In particular, it must also be true for specific values of ![]() . For example, if we ``conveniently" choose to
. For example, if we ``conveniently" choose to
let ![]() ,
,
then
![]()
so that
![]() .
.
If we choose to
let ![]() ,
,
then
![]()
so that
![]() and
and ![]() .
.
We can now say that a partial fractions decomposition for
![]() is
is
![]() .
.
If you choose to NOT use complex numbers to solve for the unknown constants in the previous example, using TWO other real values of ![]() instead of
instead of ![]() will lead to the exact same values for
will lead to the exact same values for ![]() and
and ![]() . There is one final case to consider. How should repeated factors in the denominator be handled ? The following example illustrates the partial fractions decomposition of a rational function, where the linear factor
. There is one final case to consider. How should repeated factors in the denominator be handled ? The following example illustrates the partial fractions decomposition of a rational function, where the linear factor ![]() is repeated three times and the irreducible quadratic factor
is repeated three times and the irreducible quadratic factor ![]() is repeated twice. Thus,
is repeated twice. Thus,
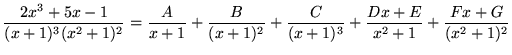 .
.
We will assume familiarity with the following rules of differentiation.
We will also assume knowledge of the following well-known, basic indefinite integral formulas :
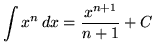 , where
, where 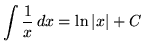
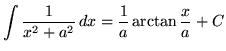
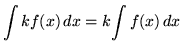 , where
, where 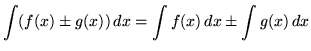
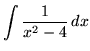 .
.
Click HERE to see a detailed solution to problem 1.
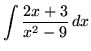 .
.
Click HERE to see a detailed solution to problem 2.
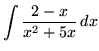 .
.
Click HERE to see a detailed solution to problem 3.
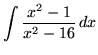 .
.
Click HERE to see a detailed solution to problem 4.
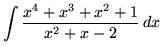 .
.
Click HERE to see a detailed solution to problem 5.
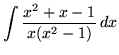 .
.
Click HERE to see a detailed solution to problem 6.
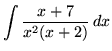 .
.
Click HERE to see a detailed solution to problem 7.
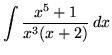 .
.
Click HERE to see a detailed solution to problem 8.
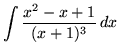 .
.
Click HERE to see a detailed solution to problem 9.
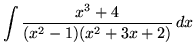 .
.
Click HERE to see a detailed solution to problem 10.
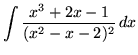 .
.
Click HERE to see a detailed solution to problem 11.
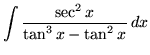 .
.
Click HERE to see a detailed solution to problem 12.
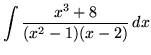 .
.
Click HERE to see a detailed solution to problem 13.
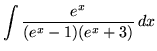 .
.
Click HERE to see a detailed solution to problem 14.
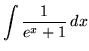 .
.
Click HERE to see a detailed solution to problem 15.
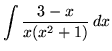 .
.
Click HERE to see a detailed solution to problem 16.
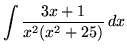 .
.
Click HERE to see a detailed solution to problem 17.
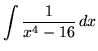 .
.
Click HERE to see a detailed solution to problem 18.
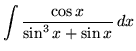 .
.
Click HERE to see a detailed solution to problem 19.
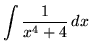 .
.
Click HERE to see a detailed solution to problem 20.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :