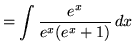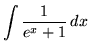Next: About this document ...



SOLUTIONS TO INTEGRATION BY PARTIAL FRACTIONS



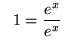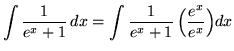
SOLUTION 15 : Integrate $ \displaystyle{ \int { 1 \over e^x + 1 } \,dx } $ . First rewrite the function by multiplying by $ \ \ 1 = \displaystyle{ e^x \over e^x } \ $ , getting truein $ \displaystyle{ \int { 1 \over e^x + 1 } \,dx } = \displaystyle{ \int { 1 \over e^x + 1 } \, \Big({ e^x \over e^x }\Big) dx } $

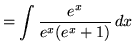$ = \displaystyle{ \int { e^x \over e^x(e^x+1) } \, dx } $ .

Now use the method of u-substitution. Let

$ u = e^x $

so that

$ du = e^x dx $ .

Substitute into the original problem, replacing all forms of $ x $, getting

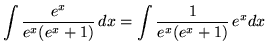
$ \displaystyle{ \int { e^x \over e^x (e^x+1) } \, dx } = \displaystyle{ \int { 1 \over e^x (e^x+1) } \, e^x dx } $

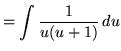
$ = \displaystyle{ \int { 1 \over u(u+1) } \, du } $

(Decompose into partial fractions.)

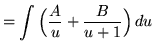
$ = \displaystyle{ \int{ \Big( {A \over u} + { B \over u+1 } \Big) } \,du } $

(After getting a common denominator, adding fractions, and equating numerators, it follows that $ \ \ A(u+1)+ Bu = 1 $ ;
let $ \displaystyle{ u = -1 : \ A(0) + B(-1) = 1 \longrightarrow B = -1 }$ ;
let $ \displaystyle{ u = 0 : \ A(1) + B(0) = 1 \longrightarrow A = 1 } $ .)

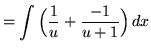
$ = \displaystyle{ \int{ \Big( {1 \over u } + { -1 \over u+1 } \Big)} \, dx} $

$ = \displaystyle{ \ln \vert u\vert - \ln \vert u+1\vert + C } $

$ = \displaystyle{ \ln \vert e^x\vert - \ln \vert e^x+1\vert + C } $

(Recall that $ \ \ln m - \ln n = \ln \Big( \displaystyle{ m \over n } \Big) $ .)

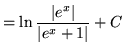$ = \displaystyle{ \ln { \vert e^x\vert \over \vert e^x+1\vert } + C } $ .

Click HERE to return to the list of problems.




SOLUTION 16 : Integrate 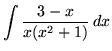$ \displaystyle{ \int { 3-x \over x(x^2+1) } \,dx } $ . Decompose into partial fractions, getting

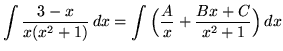
$ \displaystyle{ \int { 3 - x \over x(x^2 + 1) } \,dx} = \displaystyle{ \int{ \Big( {A \over x} + { Bx + C \over x^2 + 1} \Big) } \,dx} $

(After getting a common denominator, adding fractions, and equating numerators, it follows that $ \ \ A(x^2+1) + (Bx+C)x = 3-x $ ;
let $ \displaystyle{x = 0: A(1) + (B(0) + C) (0) = 3 \longrightarrow A = 3}$ ;
let $ \displaystyle{x = i: A(i^2+1) + (Bi + C)i = 3 - i } $
$ \longrightarrow A(-1+1) + Bi^2 + Ci = B(-1)+Ci = -B+Ci = 3-i $ ;
it follows that $ \longrightarrow B = -3 $ and $ C = - 1 $ .)

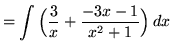
$ = \displaystyle{ \int{ \Big( {3 \over x} + { -3x - 1 \over x^2 + 1} \Big)}\,dx} $

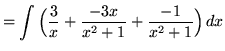
$ = \displaystyle{ \int{ \Big( {3 \over x} + {-3x \over x^2+1} + {-1 \over x^2+1} \Big) } \, dx} $

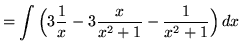
$ = \displaystyle{ \int{ \Big( 3{1 \over x} -3 { x \over x^2 + 1} - { 1 \over x^2 + 1} \Big) } \,dx } $

$ = \displaystyle{ 3 \ln{\vert x\vert} - 3 (1/2) \ln \vert x^2 + 1\vert - \arctan x + C } $

$ = \displaystyle{ 3 \ln{\vert x\vert} - {3 \over 2} \ln \vert x^2 + 1\vert - \arctan x + C } $ .

Click HERE to return to the list of problems.




SOLUTION 17 : Integrate 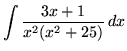$ \displaystyle{ \int {3x + 1 \over x^2 ( x^2 +25) } \,dx } $ . Decompose into partial fractions (There is a repeated linear factor !), getting

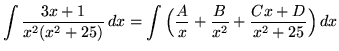
$ \displaystyle{ \int {3x + 1 \over x^2 ( x^2 +25) } \,dx } = \displaystyle{ \int { \Big({A \over x} + { B \over x^2 } + { Cx + D \over x^2 +25} \Big) } \,dx } $

(After getting a common denominator, adding fractions, and equating numerators, it follows that

$ \ \ Ax(x^2 +25) + B(x^2 + 25) + (Cx + D) x^2 = 3x + 1 $ ;

let $ \displaystyle{x = 0: \ A(0) + B(25) + (C(0)+D)(0) = 1 \longrightarrow B = {1 \over 25}}$ ;
let $ \displaystyle{x = 5i: \ A(5i)((5i)^2+25) + B((5i)^2+25) + (C(5i) + D)(5i)^2 = 15i + 1 } $
$ \longrightarrow \ A(5i)(-25+25) + B(-25+25) + (5Ci + D)(-25) = - 125Ci - 25D $ $ \ \ \ \ \ \ = 15i + 1 $ ;
it follows that $ \ -125C= 15$ and $ -25D = 1 \longrightarrow \displaystyle{ C = - {3 \over 25}} $ and $ D = \displaystyle{-{1 \over 25}} $ ;
let $ \displaystyle{x = 1: \ 26A + 26B + C + D = 4 } $
$ \longrightarrow \displaystyle{ \ 26A + {26 \over 25} - {3 \over 25} - {1 \over 25} = 26A + {22 \over 25} = 4 } $ $ \longrightarrow \displaystyle{A = (1/26){78\over 25} = {3 \over 25} } $ .)

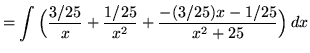
$ = \displaystyle{ \int {\Big({3/25 \over x} + { 1/25 \over x^2} + { -(3/25)x - 1/25 \over x^2+25} \Big) } \,dx } $

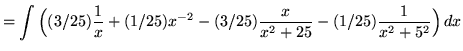
$ = \displaystyle{ \int { \Big( (3/25){1 \over x} + (1/25) x^{-2} - (3/25){ x \over x^2 +25} - (1/25) {1 \over x^2+5^2 } \Big) } \,dx } $

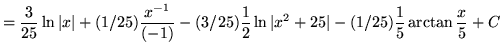
$ = \displaystyle{ {3\over 25} \ln \vert x\vert + (1/25) { x^{-1} \over (-1) } -... ...over 2} \ln {\vert x^2 +25\vert} - (1/25) {1 \over 5} \arctan {x\over 5} + C } $

$ = \displaystyle{ {3\over 25} \ln \vert x\vert - {1\over 25x} - {3 \over 50}\ln \vert x^2 +25\vert -{1 \over 125} \arctan {x\over 5} + C} $ .

Click HERE to return to the list of problems.




SOLUTION 18 : Integrate 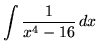$ \displaystyle{ \int{ 1 \over x^4 - 16 } \,dx } $ . Factor and decompose into partial fractions, getting

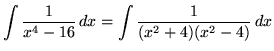
$ \displaystyle{ \int{ 1 \over x^4 - 16 } \,dx} = \displaystyle{ \int{ 1 \over (x^2 + 4)(x^2 - 4) } \,dx}$

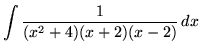
$ \displaystyle{ \int{ 1 \over (x^2 + 4)(x + 2)(x - 2) } \,dx}$

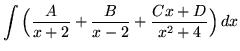
$ \displaystyle{ \int{ \Big( { A \over x+2} + { B \over x-2} + {Cx+D \over x^2+4} \Big) } \,dx}$

(After getting a common denominator, adding fractions, and equating numerators, it follows that

$ \ \ A(x-2)(x^2+4) + B(x+2)(x^2+4) + (Cx+D)(x-2)(x+2) $ $ = 1 $ ;

let $ x = 2 : \ A(0) + B(32) + (C(2)+D)(0) = 1 \longrightarrow B = \displaystyle{1 \over 32} $ ;
let $ x = -2 : \ A(-32) + B(0) + (C(-2)+D)(0) = 1 \longrightarrow A = -\displaystyle{1 \over 32} $ ;
let $ x = 2i : \ A(2i-2)((2i)^2+4) + B(2i+2)((2i)^2+4) $
$ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ + (C(2i)+D)(2i-2)(2i+2) = 1 $
$ \longrightarrow \ A(2i-2)(-4+4) + B(2i+2)(-4+4) + (2Ci+D)(4i^2-4) = 1 $
$ \longrightarrow \ (2Ci+D)(-8) = -16Ci - 8D = 1 $ ;
it follows that $ \ -16C = 0 $ and $ -8D = 1 \longrightarrow \ C = 0 $ and $ D = -\displaystyle{1 \over 8} $ .)

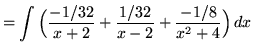
$ =\displaystyle{ \int{ \Big( { -1/32 \over x+2} + { 1/32 \over x-2} + {-1/8 \over x^2+4} \Big) } \,dx} $

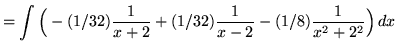
$ =\displaystyle{ \int{ \Big( -(1/32){1 \over x+2} + (1/32){1 \over x-2} - (1/8) {1 \over x^2+2^2} \Big) } \,dx} $

$ =\displaystyle{ (-1/32) \ln \vert x+2\vert + (1/32) \ln \vert x-2\vert - (1/8) {1 \over 2} \arctan {x \over 2} } + C $

$ =\displaystyle{ {1 \over 32} \Big( \ln \vert x-2\vert - \ln \vert x+2\vert \Big) - {1 \over 16} \arctan {x \over 2} } + C $

(Recall that $ \ \ln m - \ln n = \ln \Big( \displaystyle{ m \over n } \Big) $ .)

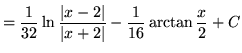$ =\displaystyle{ {1 \over 32} \ln { \vert x-2\vert \over \vert x+2\vert } - {1 \over 16} \arctan {x \over 2} } + C $ .

Click HERE to return to the list of problems.




SOLUTION 19 : Integrate 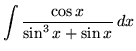$ \displaystyle{ \int{\cos x \over \sin^3 x + \sin x } \,dx } $ . Use the method of u-substitution first. Let

$ u = \sin{x} $

so that

$ du = \cos{x} \ dx $ .

Substitute into the original problem, replacing all forms of $ x $, getting

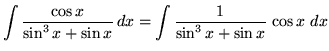
$ \displaystyle{\int {\cos x \over \sin^3 x + \sin x } \,dx } = \displaystyle{ \int {1 \over \sin^3 x + \sin x } \,\cos x \ dx} $

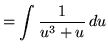
$ = \displaystyle{ \int{ 1 \over u^3 + u} \, du} $

(Factor and decompose into partial fractions.)

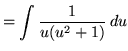
$ =\displaystyle{ \int{ 1 \over u (u^2 + 1)} \, du }$

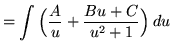
$ = \displaystyle{\int{ \Big( {A \over u} + {Bu + C \over u^2 + 1} \Big) } \, du} $

(After getting a common denominator, adding fractions, and equating numerators, it follows that $ \ \ A (u^2 +1) + (Bu + C) u = 1 $ ;
let $ u = 0: \ A(1) + 0 = 1 \longrightarrow A = 1$ ;
let $ u = i: \ A(i^2+1) + (Bi +C)i = A(0) + Bi^2 +Ci = -B +Ci = 1 $ ;
it follows that $ \ B = -1$ and $ C = 0 $ .)

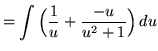
$ = \displaystyle{\int{ \Big( {1 \over u} + {-u \over u^2 + 1} \Big) } \,du} $

$ = \displaystyle{ \ln \vert u\vert - {1 \over 2} \ln \vert u^2 + 1\vert + C} $

$ = \displaystyle{ \ln \vert\sin x\vert - {1 \over 2} \ln \vert\sin^2 x + 1\vert + C} $ .

Click HERE to return to the list of problems.




SOLUTION 20 : Integrate 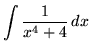$ \displaystyle{ \int{ 1 \over x^4 + 4 } \,dx } $ . Begin by rewriting the denominator by adding $ \ 0 = 4x^2 - 4x^2 $ , getting

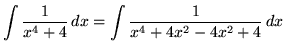
$\displaystyle{ \int{ 1 \over x^4 + 4 } \,dx} = \displaystyle{ \int{ 1 \over x^4 + 4x^2 - 4x^2 + 4 } \,dx} $

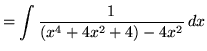
$ = \displaystyle{ \int{ 1 \over (x^4 + 4x^2 + 4) - 4x^2} \, dx} $

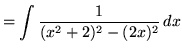
$ = \displaystyle{ \int{ 1 \over (x^2+2)^2 - (2x)^2 } \, dx} $

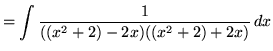
$ = \displaystyle{ \int{ 1 \over ((x^2 +2) - 2x) ((x^2 + 2) + 2x) } \, dx} $

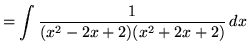
$ = \displaystyle{ \int{ 1 \over (x^2 - 2x + 2)(x^2 + 2x + 2) } \, dx} $

(The factors in the denominator are irreducible quadratic factors since they have no real roots.)

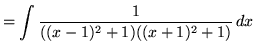
$ = \displaystyle{ \int{ 1 \over ((x-1)^2 + 1)((x+1)^2 + 1) } \, dx} $

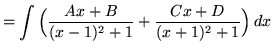
$ = \displaystyle{ \int{ \Big( { Ax+B \over (x-1)^2 + 1 } + { Cx+D \over (x+1)^2 + 1 } \Big) } \, dx} $

(After getting a common denominator, adding fractions, and equating numerators, it follows that

$ (Ax+B)((x+1)^2 + 1) + (Cx+D)((x-1)^2 + 1) $ $ = 1 $ ;

let $ x = i+1 : \ (A(i+1)+B)((i+2)^2+1) + 0 = 1 $
$ \longrightarrow ( Ai + A + B) (4i +4) = (8A+4B)i + 4B = 1 $ ;
it follows that $ \ 8A+4B = 0 $ and $ 4B = 1 \longrightarrow B = \displaystyle{1 \over 4} $ and $ A = -\displaystyle{1 \over 8} $ ;
let $ x = i-1 : \ 0 + (C(i-1)+D)((i-2)^2+1) = 1 $
$ \longrightarrow (Ci-C+D)(-4i+4) = (8C-4D)i + 4D = 1 $
it follows that $ \ 8C - 4D = 0 $ and $ 4D = 1 \longrightarrow D = \displaystyle{1 \over 4} $ and $ C = \displaystyle{1 \over 8} $ .)

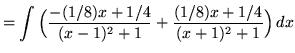
$ = \displaystyle{ \int{ \Big({ -(1/8) x + 1/4 \over (x-1)^2 + 1} + {(1/8) x + 1/4 \over (x+1)^2 + 1} \Big) } \, dx} $

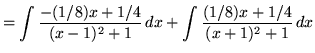$ = \displaystyle{ \int { -(1/8) x + 1/4 \over (x-1)^2 + 1 } \, dx + \int { (1/8) x + 1/4 \over (x+1)^2 + 1 } \, dx} $ .

Now use the method of substitution. In the first integral, let

$ u = x-1 $

so that

$ du = (1) \ dx = dx $ .

In the second integral, let

$ w = x+1 $

so that

$ dw = (1) \ dx = dx $ .

In addition, we can ``back substitute", using

$ x = u+1 $

in the first integral and

$ x = w-1 $

in the second integral. Now substitute into the original problems, replacing all forms of $ x $, getting

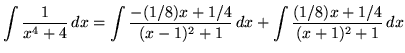
$ \displaystyle{ \int{ 1 \over x^4 + 4 } \,dx} = \displaystyle{ \int { -(1/8) ... ... \over (x-1)^2 + 1 } \, dx + \int { (1/8) x + 1/4 \over (x+1)^2 + 1 } \, dx} $

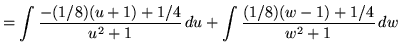
$ = \displaystyle{ \int { -(1/8) (u+1) + 1/4 \over u^2 + 1 } \, du + \int { (1/8) (w-1) + 1/4 \over w^2 + 1 } \, dw} $

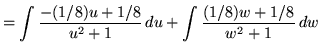
$ = \displaystyle{ \int { -(1/8) u + 1/8 \over u^2 + 1 } \, du + \int { (1/8) w + 1/8 \over w^2 + 1 } \, dw} $

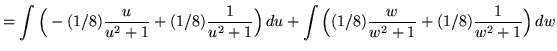
$ = \displaystyle{ \int \Big(-(1/8){ u \over u^2 + 1 } + (1/8){ 1 \over u^2 + 1 ... ...u + \int \Big( (1/8){ w \over w^2 + 1 } + (1/8){1 \over w^2 + 1 } \Big) \, dw} $

$ = \displaystyle{ -(1/8){1 \over 2} \ln \vert u^2 + 1\vert + (1/8) \arctan u } $

$ \ \ \ \ \ \ \ \ \ \ \ \ \displaystyle{+ (1/8){1 \over 2} \ln \vert w^2 + 1\vert + (1/8) \arctan w } + C $

$ = \displaystyle{ -{1 \over 16} \ln \vert(x-1)^2 + 1\vert + {1 \over 8} \arctan (x-1) } $
$ \ \ \ \ \ \ \ \ \ \ \ \ \displaystyle{+ {1 \over 16} \ln \vert(x+1)^2 + 1\vert + {1 \over 8} \arctan (x+1) } + C $

$ = \displaystyle{ -{1 \over 16} \ln \vert x^2-2x+2\vert + {1 \over 8} \arctan (x-1) } $
$ \ \ \ \ \ \ \ \ \ \ \ \ \displaystyle{ + {1 \over 16} \ln \vert x^2+2x+2\vert + {1 \over 8} \arctan (x+1) } + C $

$ = \displaystyle{ {1 \over 16} \Big( \ln \vert x^2+2x+2\vert - \ln \vert x^2-2x+2\vert \Big) } $
$ \ \ \ \ \ \ \ \ \ \ \ \ \displaystyle{+ {1 \over 8} \arctan (x-1) + {1 \over 8} \arctan (x+1) } + C $

(Recall that $ \ \ln m - \ln n = \ln \Big( \displaystyle{ m \over n } \Big) $ .)

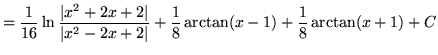$ = \displaystyle{ {1 \over 16} \ln { \vert x^2+2x+2\vert \over \vert x^2-2x+2\vert } + {1 \over 8} \arctan (x-1) + {1 \over 8} \arctan (x+1) } + C $ .

Click HERE to return to the list of problems.






Duane Kouba 2000-05-02