Solution a.): Here is a carefully labeled sketch of the region with a shell marked on the $x$-axis at $x$. Note that the height of the shell at $x$ depends on which side of 1 that $x$ lies, so that we have to split the integral into two parts ! The shell has radius $r$, measured from the $y$-axis, and height $h$, taken parallel to the $y$-axis at $x$. It is IMPORTANT to mark ALL of $x$, $r$, and $h$ in the sketch of the region !!!
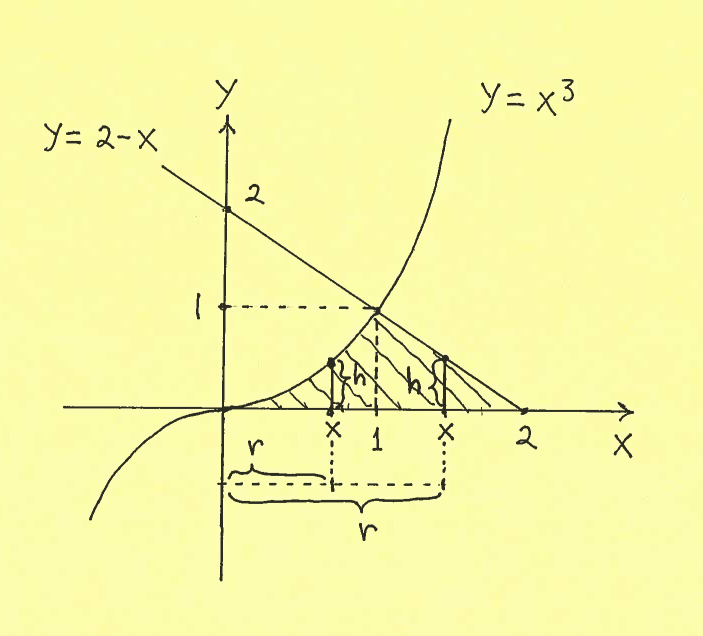
Thus the total volume of this Solid of Revolution is
$$ Volume = 2 \pi \int_{0}^{2} (radius)(height) \ dx = 2 \pi \int_{0}^{2} rh \ dx $$
$$ = 2 \pi \int_{0}^{1} rh \ dx + 2 \pi \int_{1}^{2} rh \ dx $$
$$ = 2 \pi \int_{0}^{1} (x)(x^3) \ dx + 2 \pi \int_{1}^{2} (x)(2-x) \ dx $$
Solution b.): IMPORTANT CHANGE: Because we are revolving the region about the $x$-axis, we must mark a shell on the $y$-axis at $y$ !!! The shell has radius $r$, measured from the $x$-axis, and height $h$, taken parallel to the $x$-axis at $y$. It is IMPORTANT to mark ALL of $y$, $r$, and $h$ in the sketch of the region !!!
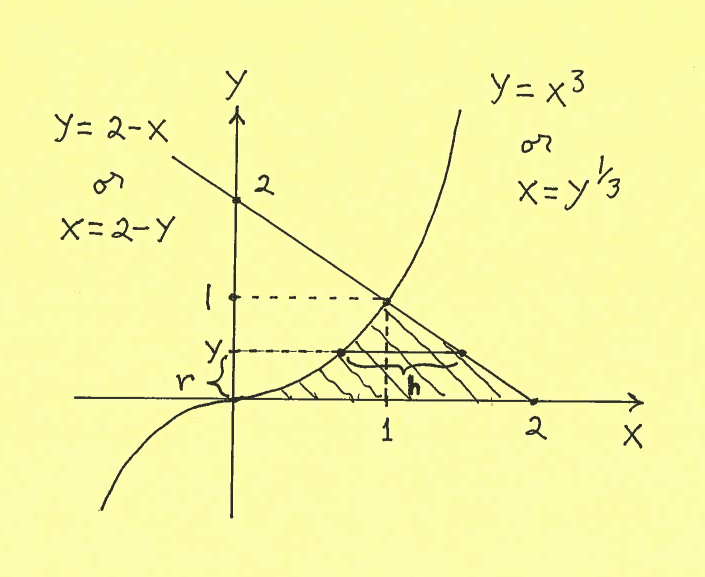
Thus the total volume of this Solid of Revolution is
$$ Volume = 2 \pi \int_{0}^{1} (radius)(height) \ dy = 2 \pi \int_{0}^{1} rh \ dy $$
$$ = 2 \pi \int_{0}^{1} (y)((2-y)-y^{1/3}) \ dy $$
Click HERE to return to the list of problems.


