COMPUTING THE VOLUME OF A SOLID OF REVOLUTION USING THE SHELL METHOD
The following problems will use the Shell Method to find the Volume of a Solid of Revolution. We start with a region $R$ in the $xy$-plane, which we "spin" around the $y$-axis to create a Solid of Revolution. Imagine the solid composed of thin concentric "shells" or cylinders, somewhat like layers of an onion, with centers of the shells being the $y$-axis. This process is called the Shell Method. The details of the Shell Method are posted below.
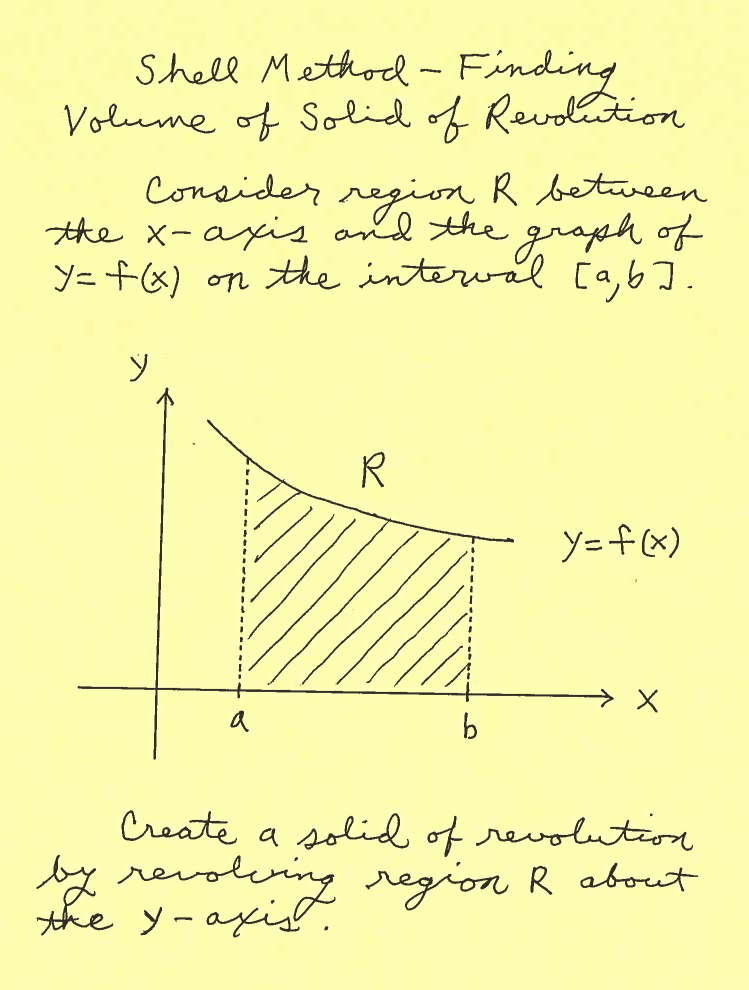
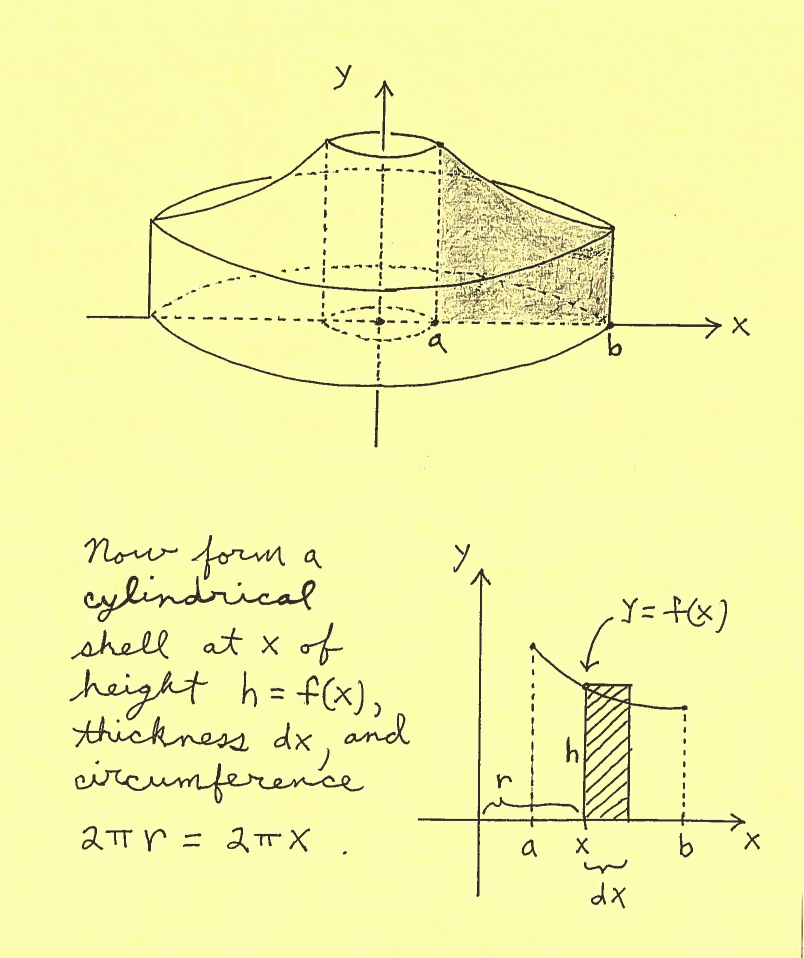
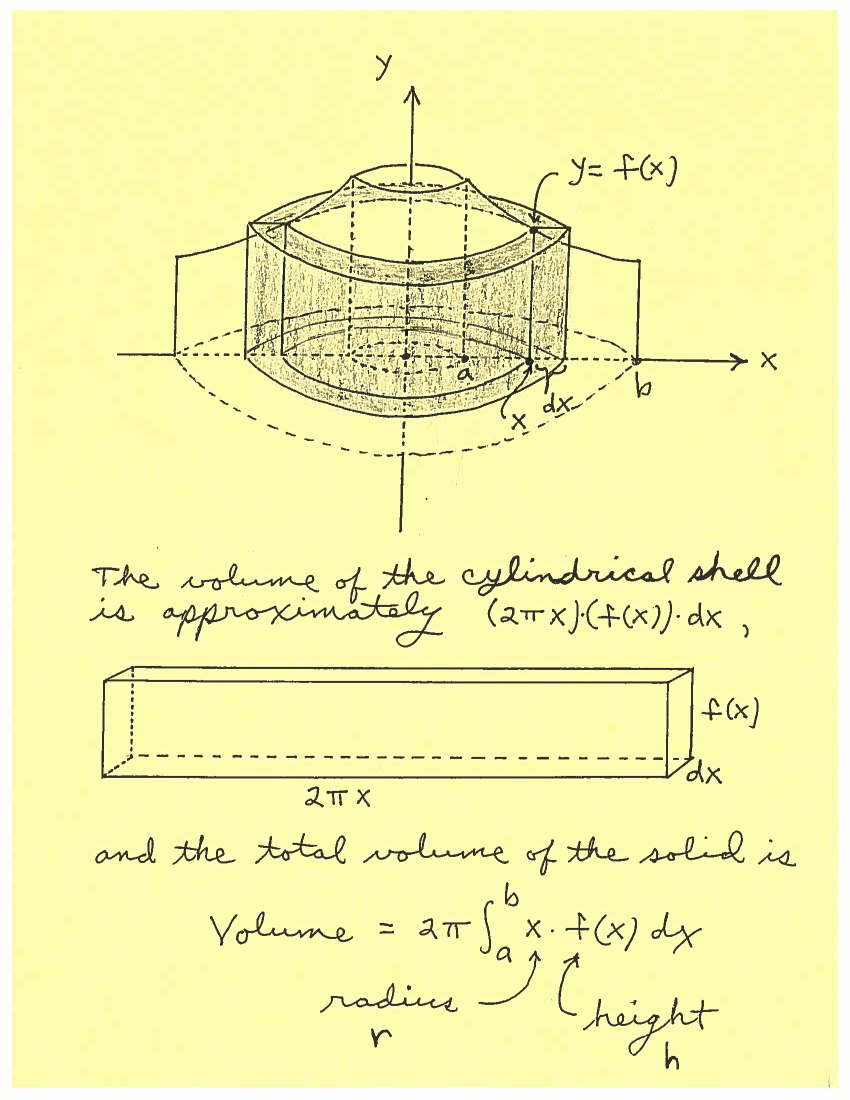
After reading the description of region $R$, we will SKETCH and CAREFULLY LABEL this region $R$. After sketching or imagining the resulting Solid of Revolution about the $y$-axis, it will be our job to create the dimensions of this cylindrical shell-- the radius $r$, measured from the $y$-axis, and the height $h$, taken parallel to the $y$-axis at $x$. The radius $r$ and height $h$ will be CAREFULLY MARKED in region $R$. This is a crucial step in the Shell Method process and is very important ! Then the Volume of the Solid of Revolution will be
$$ Volume = 2 \pi \int_{a}^{b} (radius)(height) \ dx = 2 \pi \int_{a}^{b} rh \ dx $$
We will eventually generalize the Shell Method by revolving regions $R$ about various horizontal and vertical lines, not just the $y$-axis.
EXAMPLE 1: Consider the region bounded by the graphs of $ y=\sqrt{x} $, $ y=0 $, and $ x=4 $. Use the Shell Method (SET UP ONLY) to find the Volume of the Solid formed by revolving this region about
$ \ \ \ $ a.) the $y$-axis.
$ \ \ \ $ b.) the $x$-axis.
Solution a.): Here is a carefully labeled sketch of the region with a shell marked on the $x$-axis at $x$. The shell has radius $r$, measured from the $y$-axis, and height $h$, taken parallel to the $y$-axis at $x$. It is IMPORTANT to mark ALL of $x$, $r$, and $h$ in the sketch of the region !!!
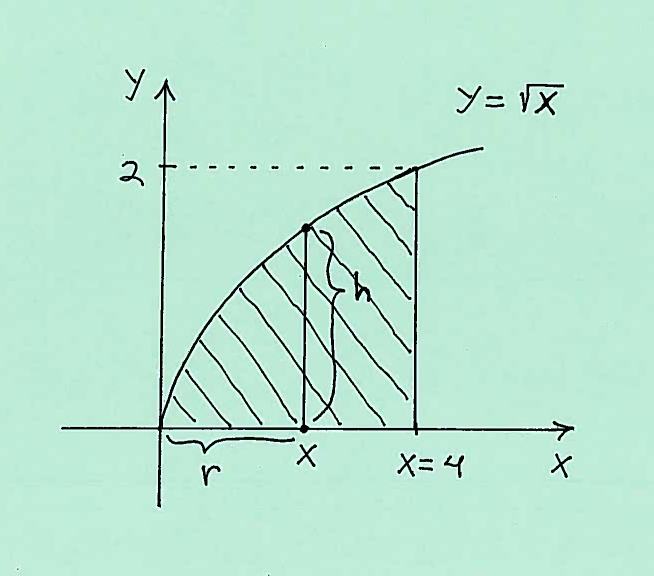
Thus the total volume of this Solid of Revolution is
$$ Volume = 2 \pi \int_{0}^{4} (radius)(height) \ dx = 2 \pi \int_{0}^{4} rh \ dx $$
$$ = 2 \pi \int_{0}^{4} (x)(\sqrt{x}) \ dx $$
Solution b.): IMPORTANT CHANGE: Here is a carefully labeled sketch of the region with a shell. Because we are revolving the region about the $x$-axis, we must mark a shell on the $y$-axis at $y$ !!! The shell has radius $r$, measured from the $x$-axis, and height $h$, taken parallel to the $x$-axis at $y$. It is IMPORTANT to mark ALL of $y$, $r$, and $h$ in the sketch of the region !!!
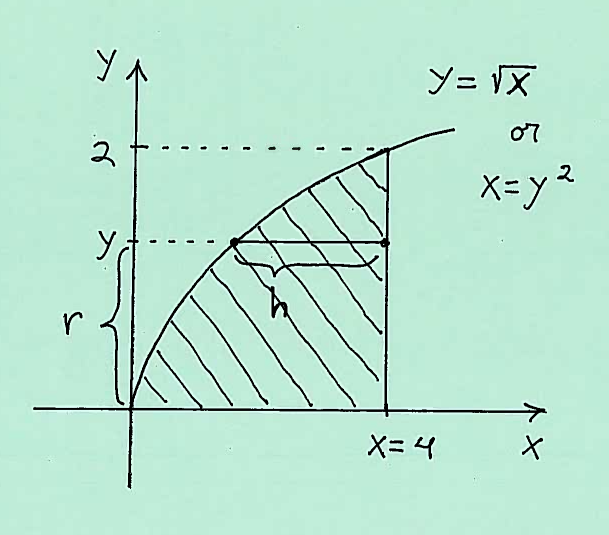
Thus the total volume of this Solid of Revolution is
$$ Volume = 2 \pi \int_{0}^{2} (radius)(height) \ dy = 2 \pi \int_{0}^{2} rh \ dy $$
$$ = 2 \pi \int_{0}^{2} (y)(4-y^2) \ dy $$
The following problems use the Shell Method to find the Volume of Solids of Revolution. Most are average. A few are somewhat challenging. All solutions SET UP the integrals but do not evaluate them. We leave the actual integration of the integrals up to you, using antiderivatives or online integrators.
- PROBLEM 1 : Consider the region bounded by the graphs of $ y= {1 \over 2}x $, $ y=3 $, and $ x=0 $. Use the Shell Method (SET UP ONLY) to find the Volume of the Solid formed by revolving this region about
$ \ \ \ $ a.) the $y$-axis.
$ \ \ \ $ b.) the $x$-axis.
Click HERE to see a detailed solution to problem 1.
- PROBLEM 2 : Consider the region bounded by the graphs of $ y= e^{x} $, $ y=e^2 $, and $ x=0 $. Use the Shell Method (SET UP ONLY) to find the Volume of the Solid formed by revolving this region about
$ \ \ \ $ a.) the $y$-axis.
$ \ \ \ $ b.) the $x$-axis.
Click HERE to see a detailed solution to problem 2.
- PROBLEM 3 : Consider the region bounded by the graphs of $ y= \ln x $, $ y=3 $, and $ x=1 $. Use the Shell Method (SET UP ONLY) to find the Volume of the Solid formed by revolving this region about
$ \ \ \ $ a.) the $y$-axis.
$ \ \ \ $ b.) the $x$-axis.
Click HERE to see a detailed solution to problem 3.
- PROBLEM 4 : Consider the region bounded by the graphs of $ y= x^3 $, $ y=2-x $, and $ y=0 $. Use the Shell Method (SET UP ONLY) to find the Volume of the Solid formed by revolving this region about
$ \ \ \ $ a.) the $y$-axis.
$ \ \ \ $ b.) the $x$-axis.
Click HERE to see a detailed solution to problem 4.
- PROBLEM 5 : Consider the region bounded by the graphs of $ y= \tan x $, $ y= \sqrt{3} $, and $ x=0 $. Use the Shell Method (SET UP ONLY) to find the Volume of the Solid formed by revolving this region about
$ \ \ \ $ a.) the $y$-axis.
$ \ \ \ $ b.) the $x$-axis.
Click HERE to see a detailed solution to problem 5.
- PROBLEM 6 : Consider the region bounded by the graphs of $ y= \sin x $ and $ y=0 $ on the interval $ [0, \pi] $. Use the Shell Method (SET UP ONLY) to find the Volume of the Solid formed by revolving this region about
$ \ \ \ $ a.) the $y$-axis.
$ \ \ \ $ b.) the $x$-axis.
Click HERE to see a detailed solution to problem 6.
- PROBLEM 7 : Consider the region bounded by the graphs of $ y= 2x $, $ y=6 $, and $ x=0 $. Use the Shell Method (SET UP ONLY) to find the Volume of the Solid formed by revolving this region about
$ \ \ \ $ a.) the $y$-axis.
$ \ \ \ $ b.) the $x$-axis.
$ \ \ \ $ c.) the line $x=-1$.
$ \ \ \ $ d.) the line $x=5$.
$ \ \ \ $ e.) the line $y=7$.
$ \ \ \ $ f.) the line $y=-2$.
Click HERE to see a detailed solution to problem 7.
- PROBLEM 8 : Consider the region bounded by the graphs of $ y= x^2 $ and $ y=8 \cdot \sqrt{x} $. Use the Shell Method (SET UP ONLY) to find the Volume of the Solid formed by revolving this region about
$ \ \ \ $ a.) the $y$-axis.
$ \ \ \ $ b.) the $x$-axis.
$ \ \ \ $ c.) the line $x=-2$.
$ \ \ \ $ d.) the line $x=6$.
$ \ \ \ $ e.) the line $y=20$.
$ \ \ \ $ f.) the line $y=-1$.
Click HERE to see a detailed solution to problem 8.
- PROBLEM 9 : Consider a circle of radius $a$ centered at the origin. Form a torus (donut) by revolving this circle about the the vertical line $ x=-b $. Use the Shell Method to find the Volume of the torus.
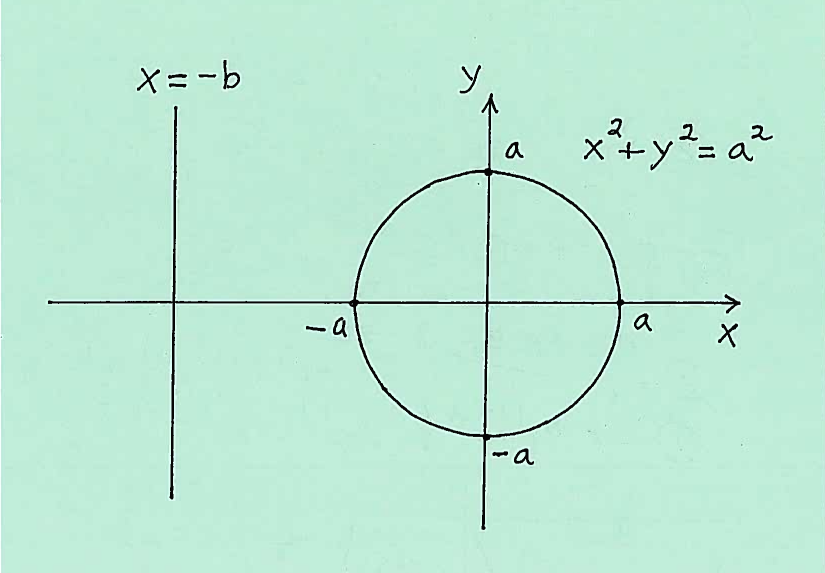
Click HERE to see a detailed solution to problem 9.
Click HERE to return to the original list of various types of calculus problems.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by
clicking on the following address :
kouba@math.ucdavis.edu
A heartfelt "Thank you" goes to The MathJax Consortium and the online Desmos Grapher for making the construction of graphs and this webpage fun and easy.
Duane Kouba ...
October 12, 2020






