Solution a.): Here is a carefully labeled sketch of the region with a shell marked on the $x$-axis at $x$. The shell has radius $r$, measured from the $y$-axis, and height $h$, taken parallel to the $y$-axis at $x$. It is IMPORTANT to mark ALL of $x$, $r$, and $h$ in the sketch of the region !!!
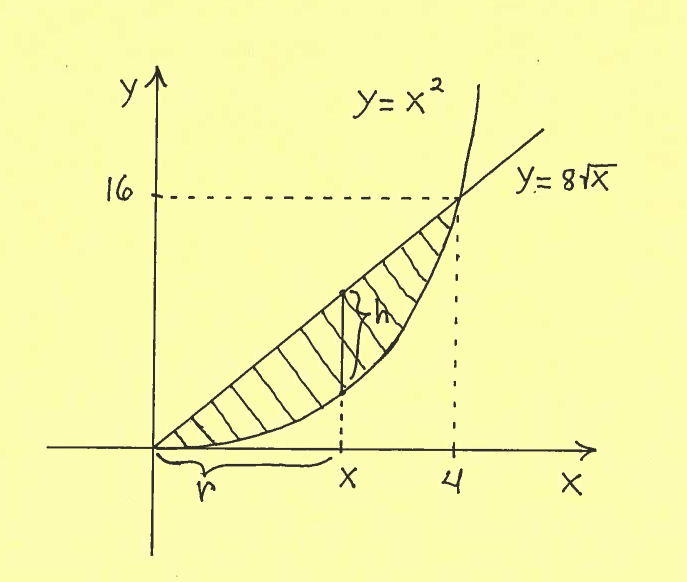
Thus the total volume of this Solid of Revolution is
$$ Volume = 2 \pi \int_{0}^{4} (radius)(height) \ dx = 2 \pi \int_{0}^{4} rh \ dx $$
$$ = 2 \pi \int_{0}^{4} (x)(8 \sqrt{x}-x^2) \ dx $$
Solution b.): IMPORTANT CHANGE: Because we are revolving the region about the $x$-axis, we must mark a shell on the $y$-axis at $y$ !!! The shell has radius $r$, measured from the $x$-axis, and height $h$, taken parallel to the $x$-axis at $y$. It is IMPORTANT to mark ALL of $y$, $r$, and $h$ in the sketch of the region !!!
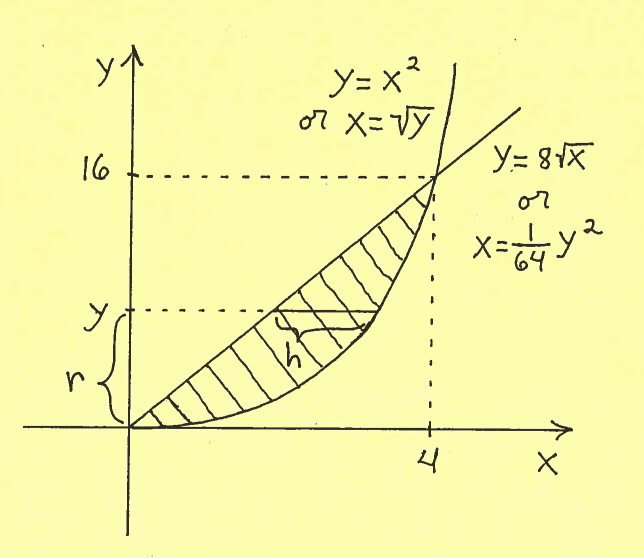
Thus the total volume of this Solid of Revolution is
$$ Volume = 2 \pi \int_{0}^{16} (radius)(height) \ dy = 2 \pi \int_{0}^{16} rh \ dy $$
$$ = 2 \pi \int_{0}^{16} (y)(\sqrt{y} - {1 \over 64}y^2) \ dy $$
Solution c.): Here is a carefully labeled sketch of the region with a shell marked on the $x$-axis at $x$. The shell has radius $r$, measured from the line $x=-2$, and height $h$, taken parallel to the $y$-axis at $x$. It is IMPORTANT to mark ALL of $x$, $r$, and $h$ in the sketch of the region !!!
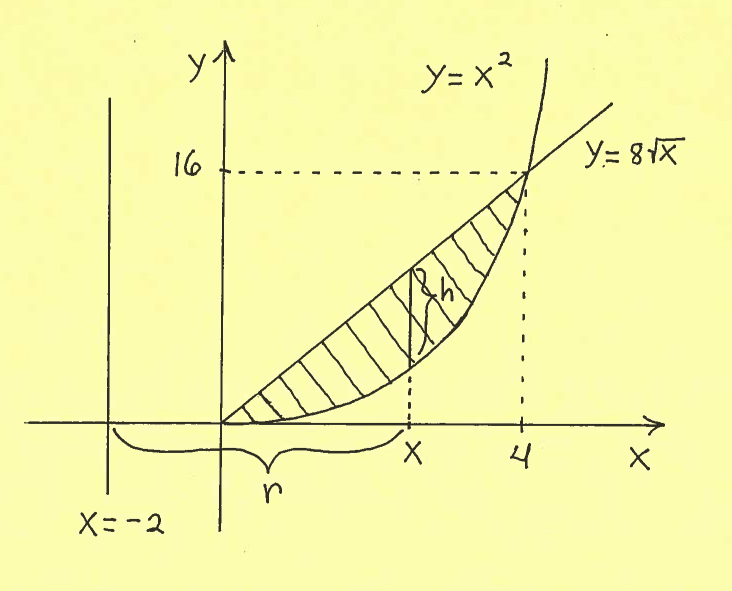
Thus the total volume of this Solid of Revolution is
$$ Volume = 2 \pi \int_{0}^{4} (radius)(height) \ dx = 2 \pi \int_{0}^{4} rh \ dx $$
$$ = 2 \pi \int_{0}^{4} (x-(-2))(8 \sqrt{x} - x^2) \ dx $$
$$ = 2 \pi \int_{0}^{4} (x+2)(8 \sqrt{x} - x^2) \ dx $$
Solution d.): Here is a carefully labeled sketch of the region with a shell marked on the $x$-axis at $x$. The shell has radius $r$, measured from the line $x=5$, and height $h$, taken parallel to the $y$-axis at $x$. It is IMPORTANT to mark ALL of $x$, $r$, and $h$ in the sketch of the region !!!
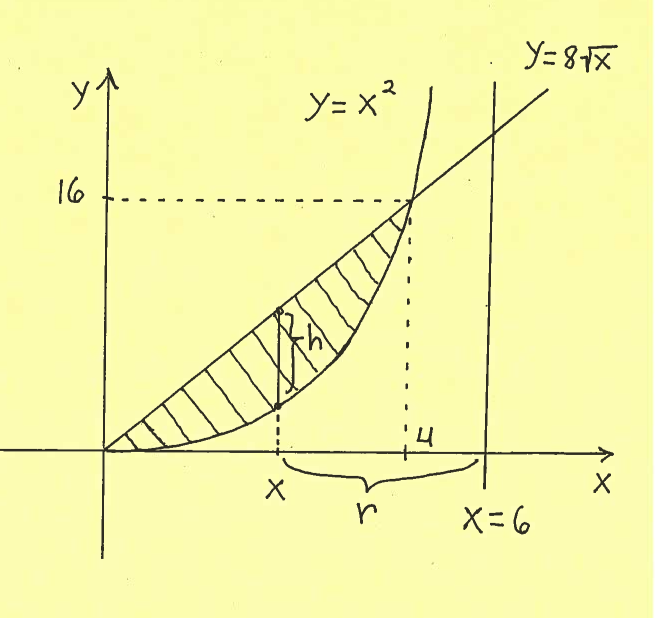
Thus the total volume of this Solid of Revolution is
$$ Volume = 2 \pi \int_{0}^{4} (radius)(height) \ dx = 2 \pi \int_{0}^{4} rh \ dx $$
$$ = 2 \pi \int_{0}^{4} (6-x)(8\sqrt{x} - x^2) \ dx $$
Solution e.): IMPORTANT CHANGE: Because we are revolving the region about the $x$-axis, we must mark a shell on the $y$-axis at $y$ !!! The shell has radius $r$, measured from the line $y=7$, and height $h$, taken parallel to the $x$-axis at $y$. It is IMPORTANT to mark ALL of $y$, $r$, and $h$ in the sketch of the region !!!
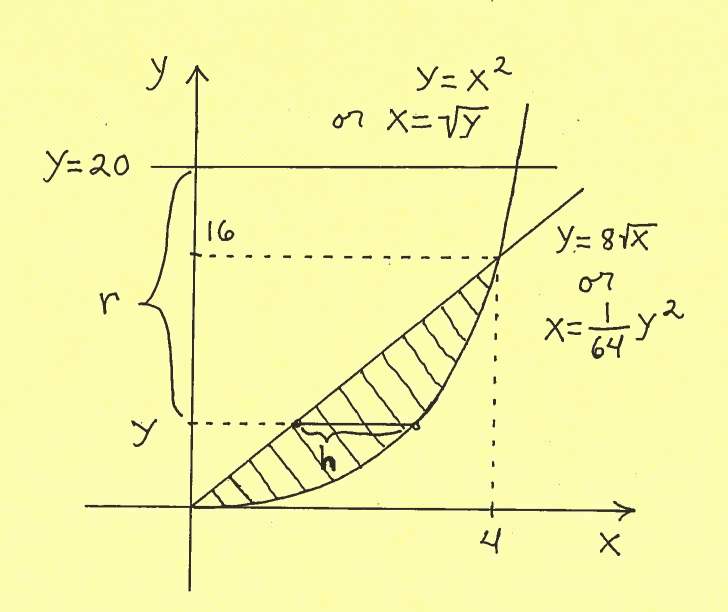
Thus the total volume of this Solid of Revolution is
$$ Volume = 2 \pi \int_{0}^{16} (radius)(height) \ dy = 2 \pi \int_{0}^{16} rh \ dy $$
$$ = 2 \pi \int_{0}^{16} (20-y)(\sqrt{y} - {1 \over 64}y^2) \ dy $$
Solution f.): IMPORTANT CHANGE: Because we are revolving the region about the $x$-axis, we must mark a shell on the $y$-axis at $y$ !!! The shell has radius $r$, measured from the line $y=-2$, and height $h$, taken parallel to the $x$-axis at $y$. It is IMPORTANT to mark ALL of $y$, $r$, and $h$ in the sketch of the region !!!
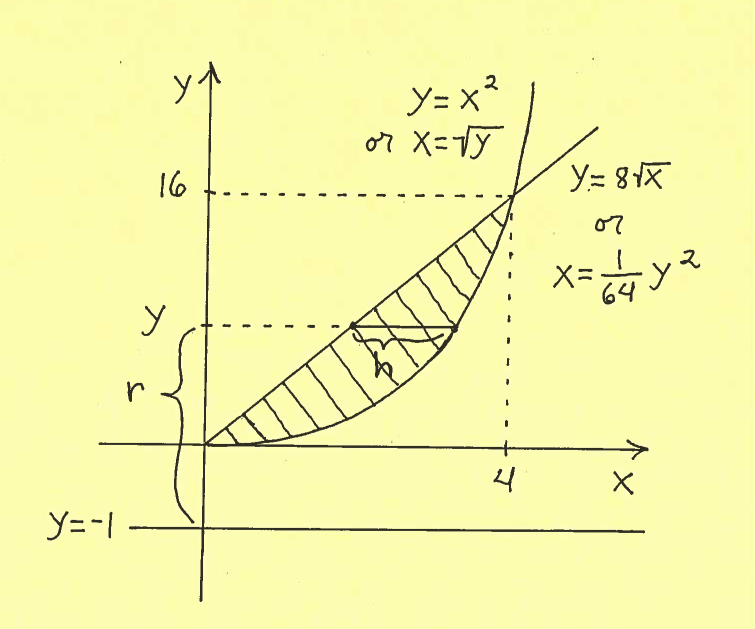
Thus the total volume of this Solid of Revolution is
$$ Volume = 2 \pi \int_{0}^{16} (radius)(height) \ dy = 2 \pi \int_{0}^{16} rh \ dy $$
$$ = 2 \pi \int_{0}^{16} (y-(-1))(\sqrt{y} - {1 \over 64}y^2) \ dy $$
$$ = 2 \pi \int_{0}^{16} (y+1)(\sqrt{y} - {1 \over 64}y^2) \ dy $$
Click HERE to return to the list of problems.






