Solution 9.): Here is a carefully labeled sketch of the circle with a shell marked on the $x$-axis at $x$. The shell has radius $r$, measured from the line $x=-b$-axis, and height $h$, taken parallel to the $y$-axis at $x$. It is IMPORTANT to mark ALL $x$, $r$, and $h$ in the sketch of the region !!!
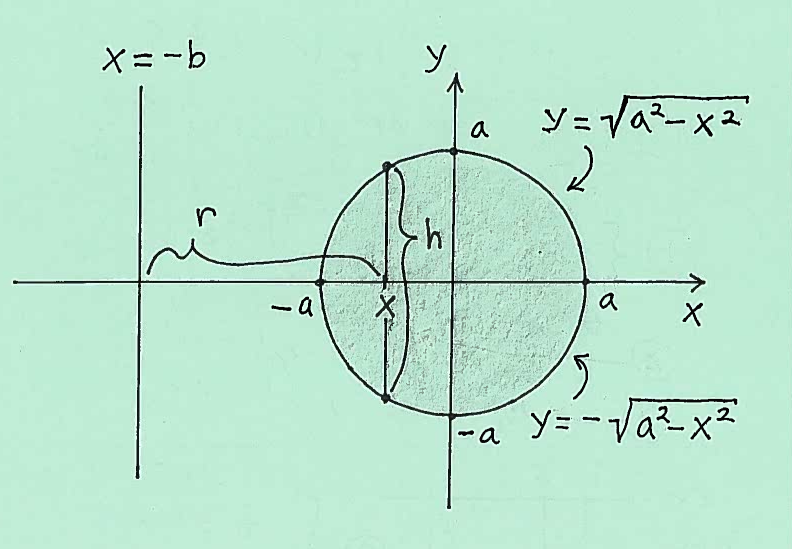
Thus the total volume of this Solid of Revolutions is
$$ Volume = 2 \pi \int_{-a}^{a} (radius)(height) \ dx = 2 \pi \int_{-a}^{a} rh \ dx $$
$$ = 2 \pi \int_{-a}^{a} (x-(-b))(\sqrt{a^2-x^2} - (- \sqrt{a^2-x^2} \ )) \ dx $$
$$ = 2 \pi \int_{-a}^{a} (x+b) (2 \cdot \sqrt{a^2-x^2} \ ) \ dx $$
$$ = 2 \pi \int_{-a}^{a} 2x \cdot \sqrt{a^2-x^2} \ dx \ \ + \ \ 2 \pi \int_{-a}^{a} 2b \cdot \sqrt{a^2-x^2} \ dx $$
$$ = 4 \pi \int_{-a}^{a} x \cdot \sqrt{a^2-x^2} \ dx \ \ + \ \ 4b \pi \int_{-a}^{a} \cdot \sqrt{a^2-x^2} \ dx $$
(Use a standard u-substitution for the first integral. Use the fact that the second integral is the area of the top semi-circle.)
$$ = 4 \pi \cdot {-1 \over 2} {2 \over 3} (a^2-x^2)^{3/2} \Big|_{-a}^{a} \ \ + \ \ 4b \pi \cdot {1 \over 2} \pi a^2 $$
$$ = {-4 \over 3} \pi ( (a^2-(a)^2)^{3/2} - (a^2-(-a)^2)^{3/2} ) \ \ + \ \ 2 \pi^2 a^2 b $$
$$ = {-4 \over 3} \pi ( 0 - 0 ) \ \ + \ \ 2 \pi^2 a^2 b $$
i.e.,
$$ Volume = 2 \pi^2 a^2 b $$
Click HERE to return to the list of problems.

