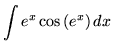 . Use u-substitution. Let
. Use u-substitution. Let
![]()
so that
![]() .
.
Substitute into the original problem, replacing all forms of ![]() , getting
, getting
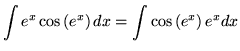
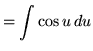
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 20 : Integrate
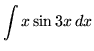 . Use integration by parts. Let
. Use integration by parts. Let
![]() and
and
![]()
so that
![]() and
and
![]() .
.
Therefore,
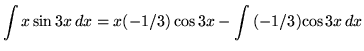
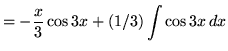
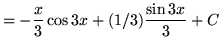
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 21 : Integrate
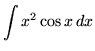 . Use integration by parts. Let
. Use integration by parts. Let
![]() and
and
![]()
so that
![]() and
and
![]() .
.
Therefore,
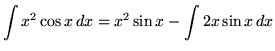
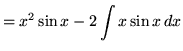 .
.
Use integration by parts again. Let
![]() and
and
![]()
so that
![]() and
and
![]() .
.
Hence,
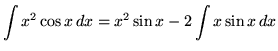
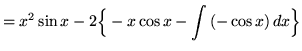
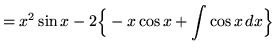
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 22 : Integrate
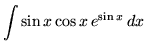 . Use u-substitution. Let
. Use u-substitution. Let
![]()
so that
![]() .
.
Substitute into the original problem, replacing all forms of ![]() , getting
, getting
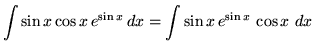
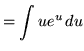 .
.
Now use integration by parts. Let
![]() and
and
![]()
so that
![]() and
and ![]() .
.
Hence,
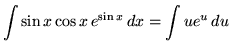
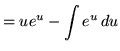
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 23 : Integrate
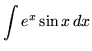 . Use integration by parts. Let
. Use integration by parts. Let
![]() and
and
![]()
so that
![]() and
and
![]() .
.
Therefore,
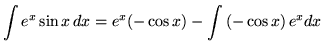
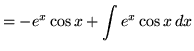 .
.
Use integration by parts again. let
![]() and
and
![]()
so that
![]() and
and
![]() .
.
Hence,
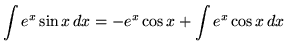
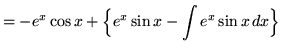
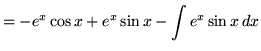 .
.
To both sides of this "equation" add
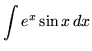 , getting
, getting
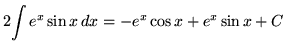 .
.
Thus,
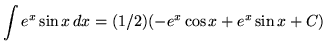
(Combine constant ![]() with
with ![]() since
since ![]() is an arbitrary constant.)
is an arbitrary constant.)
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 24 : Integrate
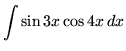 . Use integration by parts. Let
. Use integration by parts. Let
![]() and
and
![]()
so that
![]() and
and
![]() .
.
Therefore,
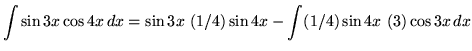
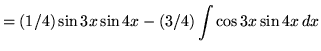 .
.
Use integration by parts again. let
![]() and
and
![]()
so that
![]() and
and
![]() .
.
Hence,
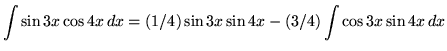
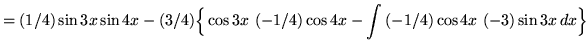
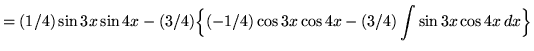
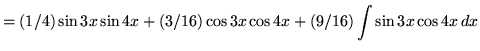 .
.
From both sides of this "equation" subtract
![]() , getting
, getting
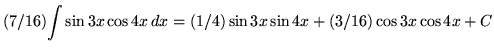 .
.
Thus,
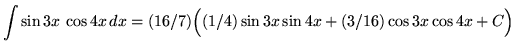
(Combine constant ![]() with
with ![]() since
since ![]() is an arbitrary constant.)
is an arbitrary constant.)
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 25 : Integrate
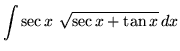 . Use u-substitution. Let
. Use u-substitution. Let
![]()
so that
![]()
![]()
![]()
![]()
![]()
![]() ,
,
or
![]() .
.
Substitute into the original problem, replacing all forms of ![]() , getting
, getting
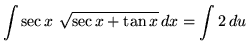
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 26 : Integrate
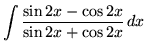 . Use u-substitution. Let
. Use u-substitution. Let
![]()
so that
![]()
![]()
![]() ,
,
or
![]() .
.
Substitute into the original problem, replacing all forms of ![]() , getting
, getting
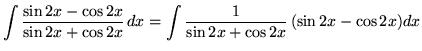
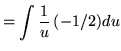
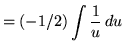
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 27 : Integrate
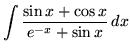 . First multiply by
. First multiply by
![]() , getting
, getting
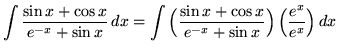
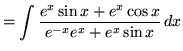 .
.
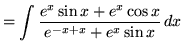 .
.
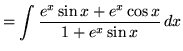 .
.
Now use u-substitution. Let
![]()
so that
![]() .
.
Substitute into the original problem, replacing all forms of ![]() , getting
, getting
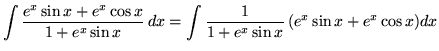
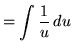
![]()
![]() .
.
Click HERE to return to the list of problems.
Next: About this document ...