Recall the definitions of the trigonometric functions.
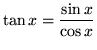
The following indefinite integrals involve all of these well-known trigonometric functions. Some of the following trigonometry identities may be needed.
It is assumed that you are familiar with the following rules of differentiation.
These lead directly to the following indefinite integrals.
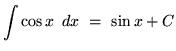
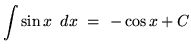
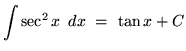
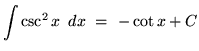
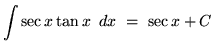
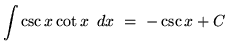
The next four indefinite integrals result from trig identities and u-substitution.
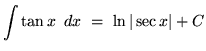
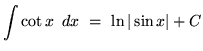
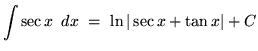
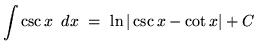
We will assume knowledge of the following well-known, basic indefinite integral formulas :
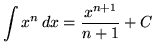 , where
, where 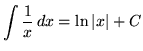
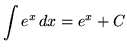
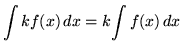 , where
, where 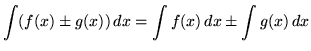
Most of the following problems are average. A few are challenging. Many use the method of u-substitution. Make careful and precise use of the differential notation ![]() and
and ![]() and be careful when arithmetically and algebraically simplifying expressions.
and be careful when arithmetically and algebraically simplifying expressions.
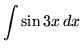 .
.
Click HERE to see a detailed solution to problem 1.
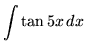 .
.
Click HERE to see a detailed solution to problem 2.
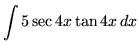 .
.
Click HERE to see a detailed solution to problem 3.
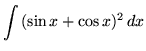 .
.
Click HERE to see a detailed solution to problem 4.
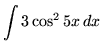 .
.
Click HERE to see a detailed solution to problem 5.
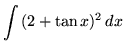 .
.
Click HERE to see a detailed solution to problem 6.
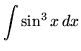 .
.
Click HERE to see a detailed solution to problem 7.
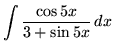 .
.
Click HERE to see a detailed solution to problem 8.
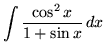 .
.
Click HERE to see a detailed solution to problem 9.
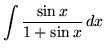 .
.
Click HERE to see a detailed solution to problem 10.
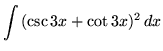 .
.
Click HERE to see a detailed solution to problem 11.
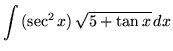 .
.
Click HERE to see a detailed solution to problem 12.
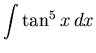
Click HERE to see a detailed solution to problem 13.
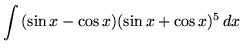 .
.
Click HERE to see a detailed solution to problem 14.
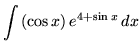 .
.
Click HERE to see a detailed solution to problem 15.
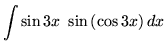 .
.
Click HERE to see a detailed solution to problem 16.
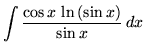 .
.
Click HERE to see a detailed solution to problem 17.
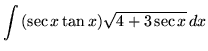 .
.
Click HERE to see a detailed solution to problem 18.
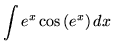 .
.
Click HERE to see a detailed solution to problem 19.
Some of the following problems require the method of integration by parts. That is,
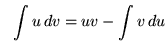 .
.
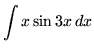 .
.
Click HERE to see a detailed solution to problem 20.
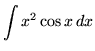 .
.
Click HERE to see a detailed solution to problem 21.
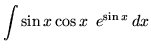 .
.
Click HERE to see a detailed solution to problem 22.
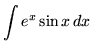 .
.
Click HERE to see a detailed solution to problem 23.
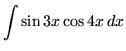 .
.
Click HERE to see a detailed solution to problem 24.
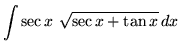 .
.
Click HERE to see a detailed solution to problem 25.
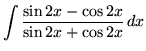 .
.
Click HERE to see a detailed solution to problem 26.
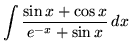 .
.
Click HERE to see a detailed solution to problem 27.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :