SOLUTION 14: $ \ \ $ Integrate $ \displaystyle{ \int { x
\cdot \sqrt{10x-x^2} } \ dx } $. First complete the square.
$$ = \displaystyle { \int x \cdot \sqrt{10x-x^{2}} \ dx = \int x
\cdot \sqrt{-(x^{2}-10x)} \ dx } $$
$$ = \displaystyle { \int x \cdot \sqrt{-(x^{2}-10x+25)+25} \ dx } $$
$$ = \displaystyle { \int x \cdot \sqrt{-(x-5)^{2}+25} \ dx } $$
Now use the trig substitution
$$ x-5 = 5 \sin \theta $$
so that
$$ dx = 5 \cos \theta \ d\theta $$
Substitute into the original problem, replacing all
forms of x, getting
$$ \displaystyle { \int x \cdot \sqrt{-(x-5)^{2}+25} \ dx }
= \displaystyle { \int (5 + 5 \sin \theta) \cdot \sqrt {-25
\sin^{2} \theta + 25} \cdot 5 \cos \theta \ d \theta } $$
$$ = \displaystyle { \int (5 + 5 \sin \theta) \cdot \sqrt {25
(1-\sin^{2} \theta) } \cdot 5 \cos \theta \ d \theta } $$
$$ = \displaystyle { \int (5 + 5 \sin \theta) \cdot \sqrt{25
\cos^{2} \theta} \cdot 5 \cos \theta \ d \theta } $$
$$ = \displaystyle { \int 5(1+ \sin \theta) \cdot 5 \cos \theta
\cdot 5 \cos \theta \ d \theta } $$
$$ = \displaystyle { 125 \int (1 + \sin \theta) \cos^{2} \theta \ d
\theta } $$
$$ = \displaystyle { 125 \int (\cos^{2} \theta + \sin \theta
\cos^{2} \theta) \ d \theta } $$
$$ = \displaystyle { 125 \int \cos^{2} \theta \ d \theta + 125 \int
\sin \theta \cos^{2} \theta \ d \theta } $$
$\Bigg( $ Let $ A = \displaystyle { \int \cos^{2} \theta \ d
\theta } \ $ and recall that $ \ \cos 2 \theta = 2 \cos^{2} \theta - 1 \ $ so that
$ \cos^{2} \theta = (1/2) \cos 2 \theta \ $. Then
$$ \displaystyle { A = \int \frac{\cos 2 \theta + 1}{2} \ d \theta } $$
$$ = \displaystyle { \int \Big( \frac{1}{2} \cos 2 \theta + \frac{1}{2} \Big) \ d \theta } $$
$$ = \displaystyle { \frac{1}{2} \frac{\sin 2 \theta}{2} + \frac{\theta}{2} + C} $$
$$ = \displaystyle { \frac{\sin 2 \theta}{4} + \frac{\theta}{2} + C} $$
Let $ B = \int \sin \theta \cos^{2} \theta \ d \theta
$. $ \ $ Use the ordinary u-ubstitution
$$ u = \cos \theta $$
so that
$$ du = - \sin \theta \ d \theta \ \ \longrightarrow \ \ - du = \sin \theta \ d \theta $$
Substitute into the original problem, replacing all
forms of $ u $, getting
$$ \displaystyle { \int \sin \theta \cos^{2} \theta \ d \theta
= \int -u^{2} \ d \theta } $$
$$ = \displaystyle { - \frac{u^{3}}{3} + C} $$
$$ = \displaystyle { - \frac{\cos^{3} \theta}{3} + C } \ \Bigg) $$
$$ = 125 A + 125 B $$
$$ = \displaystyle { 125 \Big( \frac{\sin 2 \theta}{4} + \frac{\theta}{2} \Big) -
125 \Big(- \frac{\cos^{3} \theta}{3} \Big)+ C } $$
(Recall that $ \sin 2 \theta = 2 \sin \theta \cos \theta $. )
$$ = \displaystyle { \frac{125}{4} (2 \sin \theta \cos \theta) +
\frac{125}{2} \theta + \frac{125}{3} \cos^{3} \theta + C } $$
$$ = \displaystyle { \frac{125}{2} \sin \theta \cos \theta +
\frac{125}{2} \theta + \frac{125}{3} \cos^{3} \theta + C } $$
$\Big($ We need to write our final answer in terms of $x$.
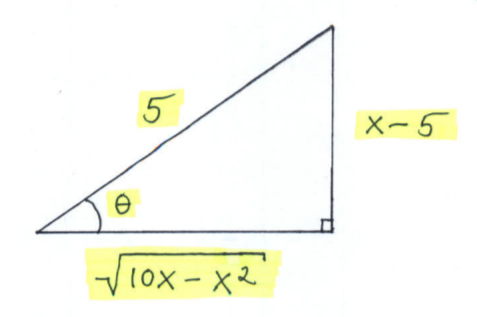
Since $ \ x-5 = 5 \sin \theta \ $ it follows that
$ \ \theta = \arcsin \displaystyle{ x-5 \over 5 } \ $ and
$$ \sin \theta = \displaystyle{ x-5 \over 5 } = \displaystyle{ opposite \over hypotenuse } $$
and from the Pythagorean Theorem that
$$ \displaystyle (adjacent)^2 + (opposite)^2 = (hypotenuse)^2
\ \ \longrightarrow $$
$$ (adjacent)^2 + (x-5)^2 = (5)^2
\ \ \longrightarrow \ \ \ adjacent = \sqrt{25-(x-5)^2} = \sqrt{10x-x^2} \ \ \longrightarrow $$
$$ \cos \theta = \displaystyle{ adjacent \over hypotenuse }= \displaystyle{ \sqrt{10x-x^2} \over 5 }. \Big) $$
$$ = \displaystyle { \frac{125}{2} \cdot \frac{x-5}{5} \cdot \frac{\sqrt{10x-x^2}}{5} +
\frac{125}{2} \cdot \arcsin \frac{x-5}{10} -
\frac{125}{3}\Big(\frac{\sqrt{10x-x^2}}{5} \Big)^{3} + C } $$
$$ = \displaystyle { \frac{5}{2} (x-5) \sqrt{10x-x^2} +
\frac{125}{2} \arcsin \frac{x-5}{10} - \frac{1}{3} (10x-x^2)^{3/2} + C } $$
Click HERE to return to the list of problems.

