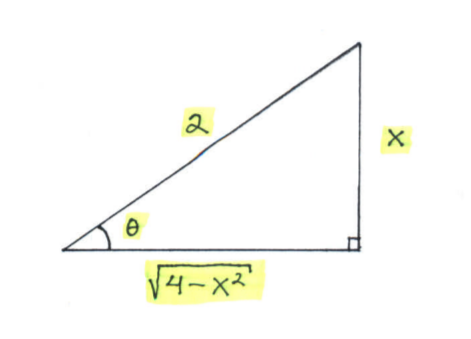
- PROBLEM 1 : Integrate $ \displaystyle{ \int { \sqrt{1-x^2} } \,dx } $
Click HERE to see a detailed solution to problem 1.
- PROBLEM 2 : Integrate $ \displaystyle{ \int { (x^2-1)^{3/2} \over x } \, dx } $ .
Click HERE to see a detailed solution to problem 2.
- PROBLEM 3 : Integrate $ \displaystyle{ \int { 1 \over (1-x^2)^{3/2} } \, dx } $ .
Click HERE to see a detailed solution to problem 3.
- PROBLEM 4 : Integrate $ \displaystyle{ \int { \sqrt{x^2+1} \over x } \, dx } $ .
Click HERE to see a detailed solution to problem 4.
- PROBLEM 5 : Integrate $ \displaystyle{ \int x^3 \sqrt{4-9x^2} \, dx } $ .
Click HERE to see a detailed solution to problem 5.
- PROBLEM 6 : Integrate $ \displaystyle{ \int { \sqrt{1-x^2} \over x } \, dx } $ .
Click HERE to see a detailed solution to problem 6.
- PROBLEM 7 : Integrate $ \displaystyle{ \int { \sqrt{x^2-9} \over x^2 } \, dx } $ .
Click HERE to see a detailed solution to problem 7.
- PROBLEM 8 : Integrate $ \displaystyle{ \int { \sqrt{x^2+1} \over x^2 } \,dx } $ .
Click HERE to see a detailed solution to problem 8.
- PROBLEM 9 : Integrate $ \displaystyle{ \int \sqrt{x^2+25 } \,dx } $ .
Click HERE to see a detailed solution to problem 9.
- PROBLEM 10 : Integrate $ \displaystyle{ \int { \sqrt{x^2-4} } \,dx } $ .
Click HERE to see a detailed solution to problem 10.
- PROBLEM 11 : Integrate $ \displaystyle{ \int { x \over \sqrt{x^4-16} } \, dx } $ .
Click HERE to see a detailed solution to problem 11.
- PROBLEM 12 : Integrate $ \displaystyle{ \int { 1 \over \sqrt{x^2-4x} } \, dx } $ .
Click HERE to see a detailed solution to problem 12.
- PROBLEM 13 : Integrate $ \displaystyle{ \int { x \over \sqrt{x^2+4x+5} } \, dx } $ .
Click HERE to see a detailed solution to problem 13.
- PROBLEM 14 : Integrate $ \displaystyle{ \int { x \cdot \sqrt{10x-x^2} } \, dx } $ .
Click HERE to see a detailed solution to problem 14.
- PROBLEM 15 : Integrate $ \displaystyle{ \int { \sqrt{ {x-1} \over x } } \, dx } $ .
Click HERE to see a detailed solution to problem 15.
- PROBLEM 16 : Integrate $ \displaystyle{ \int { \sqrt{1-x} \cdot \sqrt{x+3} } \, dx } $ .
Click HERE or HERE to see a detailed solution to problem 16.
- PROBLEM 17 : A motorboat is resting at the origin, $(0, 0)$, and a skier tethered to the boat with a 20-foot long rope, is resting at the point $(20, 0)$. The boat then begins moving along the positive $y$-axis, pulling the skier along the unknown path $y=f(x)$. Use integration to find an equation for this path.
Click HERE to see a detailed solution to problem 17.
Click HERE to return to the original list of various types of calculus problems.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by
clicking on the following address :
kouba@math.ucdavis.edu
A heartfelt "Thank you" goes to The MathJax Consortium and the online Desmos Grapher for making the construction of graphs and this webpage fun and easy.
Duane Kouba ...
May 31, 2017