SOLUTION 17: $ \ \ $ A motorboat is resting at the origin, $(0,
0)$, and a skier tethered to the boat with a 20-foot long rope, is
resting at the point $(20, 0)$. (See the diagram below.)
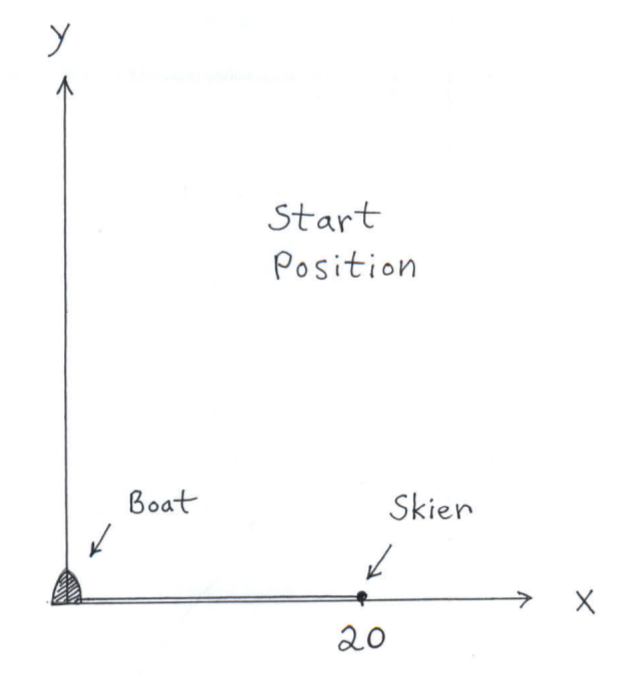
The boat then begins moving along
the positive $y$-axis, pulling the skier along the unknown path
$y=f(x)$. Use integration to find an equation for this path. We will assume that the 20-foot rope lies on a tangent line to the unknown curve $ y=f(x) $ at the point of tangency at $ (x,y) $ (The point $ (x,y) $ represents the skier.). Consider the right triangle formed by the boat on the $y$-axis, the skier on the curve at the point $ (x,y) $, and the point $ (0,y) $. The base of this right triangle is $x$. The hypotenuse of this right triangle is 20. Let $L$ be the height of this right triangle. (See the diagrams below.)
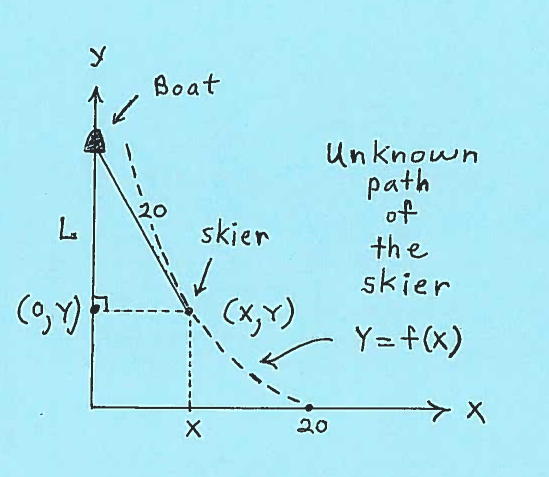
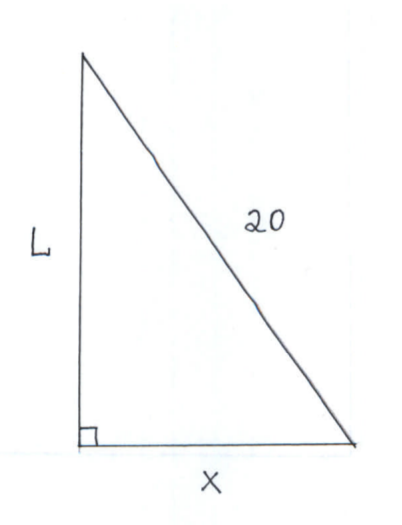
By the Pythagorean Theorem we get that
$$ x^2+L^2 = 20^2 \ \ \longrightarrow \ \ \ L = \sqrt{ 400-x^2 } $$
Since the hypotenuse is on the tangent line to the unknown curve $ y=f(x) $, it follows that the slope of the tangent line is
$$ f'(x) = slope = \displaystyle {\frac {rise}{run}} = \displaystyle {\frac {-L}{x}}
= \displaystyle {\frac {-\sqrt{ 400-x^2 }}{x}} $$
so that the unknown curve is
$$ f(x) = \displaystyle { \int \frac {-\sqrt{ 400-x^2 }}{x} \ dx }
= \displaystyle { - \int \frac {\sqrt{ 400-x^2 }}{x} \ dx } $$
together with the fact that $ f(20)=0 $ (position of skier before boat takes off). Begin the integration with the trig substitution
$$ x = 20 \sin \theta $$
so that
$$ dx = 20 \cos \theta \ d \theta $$
Substitute into the original problem, replacing all
forms of x, getting
$$ \displaystyle { - \int \frac {\sqrt{ 400-x^2 }}{x} \ dx }
= \displaystyle { - \int \frac {\sqrt{ 400-(20 \sin \theta)^2 }}{20 \sin \theta} \cdot 20 \cos \theta \ d \theta } $$
$$ = \displaystyle { - \int \frac {\sqrt{ 400-400 \sin^2 \theta }}{ \sin \theta} \cdot \cos \theta \ d \theta } $$
$$ = \displaystyle { - \int \frac {\sqrt{ 400(1- \sin^2 \theta) }}{ \sin \theta} \cdot \cos \theta \ d \theta } $$
$$ = \displaystyle { - \int \frac {20 \sqrt{1- \sin^2 \theta }}{ \sin \theta} \cdot \cos \theta \ d \theta } $$
$$ = \displaystyle { - 20 \int \frac { \sqrt{ \cos^2 \theta }}{ \sin \theta} \cdot \cos \theta \ d \theta } $$
$$ = \displaystyle { - 20 \int \frac { \cos \theta }{ \sin \theta} \cdot \cos \theta \ d \theta } $$
$$ = \displaystyle { - 20 \int \frac { \cos^2 \theta }{ \sin \theta} \ d \theta } $$
(Recall that $ \cos^2 \theta + \sin^2 \theta = 1 $ so that $ \cos^2 \theta = 1 - \sin^2 \theta $.)
$$ = \displaystyle { - 20 \int \frac { 1 - \sin^2 \theta }{ \sin \theta} \ d \theta } $$
$$ = \displaystyle { - 20 \int \Big( \frac { 1 }{ \sin \theta}
- \frac { \sin^2 \theta }{ \sin \theta} \Big) \ d \theta } $$
$$ = \displaystyle { - 20 \int ( \csc \theta - \sin \theta ) \ d \theta } $$
$$ = \displaystyle { - 20 ( \ln \Big| \csc \theta - \cot \theta \Big| + \cos \theta ) + C } $$
$\Big($ We need to write our final answer in terms of $x$.
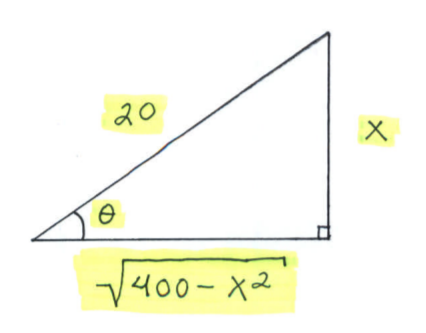
Since $ x = 20 \sin \theta $ it follows that
$$ \sin \theta = \displaystyle{ x \over 20 } = \displaystyle{ opposite \over hypotenuse } $$
and from the Pythagorean Theorem that
$$ \displaystyle (adjacent)^2 + (opposite)^2 = (hypotenuse)^2
\ \ \longrightarrow $$
$$ (adjacent)^2 + (x)^2 = (20)^2
\ \ \longrightarrow \ \ \ adjacent = \sqrt{400-x^2} \ \ \longrightarrow $$
$$ \cos \theta = \displaystyle{ adjacent \over hypotenuse }= \displaystyle{ \sqrt{400-x^2} \over 20 } $$
$$ \cot \theta = \displaystyle{ adjacent \over opposite }= \displaystyle{ \sqrt{400-x^2} \over x } $$
and
$$ \csc \theta = \displaystyle{ hypotenuse \over opposite }= \displaystyle{ 20 \over x } . \Big) $$
$$ = \displaystyle { - 20 ( \ln \Big| { 20 \over x } - { \sqrt{400-x^2} \over x } \Big| + { \sqrt{400-x^2} \over 20 } ) + C } $$
$$ = \displaystyle { - 20 \ln \Big| { 20 - \sqrt{400-x^2} \over x } \Big| - \sqrt{400-x^2} + C } $$
i.e.,
$$ f(x) = \displaystyle { - 20 \ln \Big| { 20 - \sqrt{400-x^2} \over x } \Big| - \sqrt{400-x^2} + C } $$
Since $ f(20)=0 $, we get that
$$ f(20) = \displaystyle { - 20 \ln \Big| { 20 - \sqrt{400-(20)^2} \over 20 } \Big| - \sqrt{400-(20)^2} + C }
\ \ \longrightarrow $$
$$ 0 = \displaystyle { - 20 \ln \Big| { 20 - 0 \over 20 } \Big| - \sqrt{400-(20)^2} + C }
\ \ \longrightarrow $$
$$ 0 = \displaystyle { - 20 \ln 1 - \sqrt{0} + C }
\ \ \longrightarrow $$
$$ 0 = \displaystyle { - 20 (0) + C }
\ \ \longrightarrow $$
$$ C=0 $$
Thus, the skier follows the curve given by
$$ f(x) = \displaystyle { - 20 \ln \Big| { 20 - \sqrt{400-x^2} \over x } \Big| - \sqrt{400-x^2} } $$
Click HERE to return to the list of problems.




