-
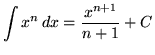
-
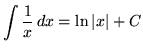
-
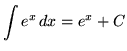
-
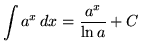 , where a is a constant
, where a is a constant
-
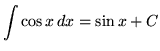
-
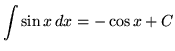
-
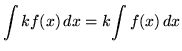 , where k is a constant
, where k is a constant
-
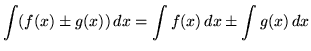
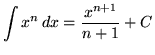
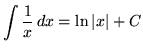
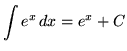
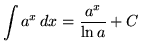 , where a is a constant
, where a is a constant
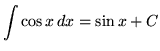
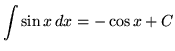
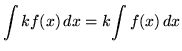 , where k is a constant
, where k is a constant
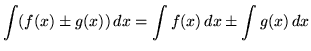
![]() ,
,
it follows easily that
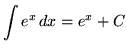 .
.
However, it may not be obvious to some how to integrate
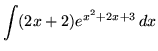 .
.
Note that the derivative of
![]() can be computed using the chain rule and is
can be computed using the chain rule and is
![]()
![]()
![]() .
.
Thus, it follows easily that
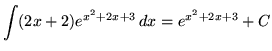 .
.
This is an illustration of the chain rule "backwards". Now the method of u-substitution will be illustrated on this same example. Begin with
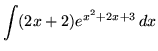 ,
,
and let
u = x2+2x+3 .
Then the derivative of u is
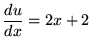 .
.
Now "pretend" that the differentiation notation
![]() is an arithmetic fraction, and multiply both sides of the previous equation by dx getting
is an arithmetic fraction, and multiply both sides of the previous equation by dx getting
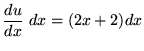
or
du = (2x+2) dx .
Make substitutions into the original problem, removing all forms of x , resulting in
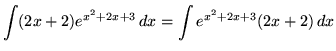
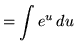
= e u + C
= e x2+2x+3 + C .
Of course, it is the same answer that we got before, using the chain rule "backwards". In essence, the method of u-substitution is a way to recognize the antiderivative of a chain rule derivative. Here is another illustraion of u-substitution. Consider
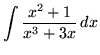 .
.
Let
u = x3+3x .
Then (Go directly to the du part.)
du = (3x2+3) dx = 3(x2+1) dx ,
so that
(1/3) du = (x2+1) dx .
Make substitutions into the original problem, removing all forms of x , resulting in
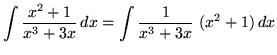
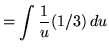
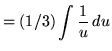
![]()
![]() .
.
Most of the following problems are average. A few are challenging. Make careful and precise use of the differential notation dx and du and be careful when arithmetically and algebraically simplifying expressions.
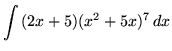 .
.
Click HERE to see a detailed solution to problem 1.
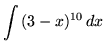 .
.
Click HERE to see a detailed solution to problem 2.
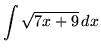 .
.
Click HERE to see a detailed solution to problem 3.
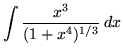 .
.
Click HERE to see a detailed solution to problem 4.
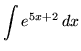 .
.
Click HERE to see a detailed solution to problem 5.
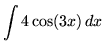 .
.
Click HERE to see a detailed solution to problem 6.
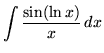 .
.
Click HERE to see a detailed solution to problem 7.
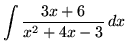 .
.
Click HERE to see a detailed solution to problem 8.
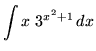 .
.
Click HERE to see a detailed solution to problem 9.
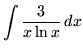 .
.
Click HERE to see a detailed solution to problem 10.
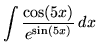 .
.
Click HERE to see a detailed solution to problem 11.
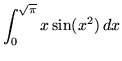 .
.
Click HERE to see a detailed solution to problem 12.
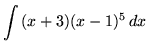 .
.
Click HERE to see a detailed solution to problem 13.
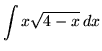 .
.
Click HERE to see a detailed solution to problem 14.
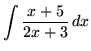 .
.
Click HERE to see a detailed solution to problem 15.
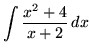 .
.
Click HERE to see a detailed solution to problem 16.
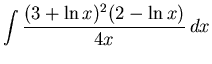 .
.
Click HERE to see a detailed solution to problem 17.
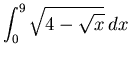 .
.
Click HERE to see a detailed solution to problem 18.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :