From Fourier expansions to Gabor expansions

Motivated by the study of heat diffusion, Fourier asserted that an arbitrary function $ f$ in $ [0,1)$ could be represented by a trigonometric series

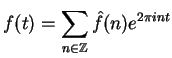$\displaystyle f(t) = \sum_{n \in \Z} \hat{f}(n) e^{2\pi int}$    

where

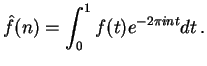$\displaystyle \hat{f}(n) = \int_{0}^{1} f(t) e^{-2\pi int} dt\,.$    

A good part of mathematical analysis developed since then was devoted to the attempt to make Fourier's statement precise. Despite the delicate problems of convergence, Fourier series are a powerful and widely used tool in mathematics, engineering, physics, and other areas. The existence of the Fast Fourier Transform has extended this use enormously in the past thirty years. Fourier expansions are not only useful to study single functions or function spaces, they can also be applied to study operators between function spaces. It is a well-known fact that the trigonometric basis $ \{e^{2\pi i nt} , n \in \Z\}$ diagonalizes translation invariant operators on the interval $ [0,1)$, identified with the torus.

However the Fourier system is not adapted to represent local information in time of a function or an operator, since the representation functions themselves are not at all localized in time, we have $ \vert e^{2 \pi i nt}\vert =1$ for all $ n$ and $ t$. A local perturbation of $ f(t)$ may result in a perturbation of all expansion coefficients $ \hat{f}(\omega)$. Roughly speaking the same remarks apply to the Fourier transform. The Fourier transform is an ideal tool to study stationary signals and processes (where the properties are statistically invariant over time). However many physical processes and signals are nonstationary, they evolve with time, such as speech or music.

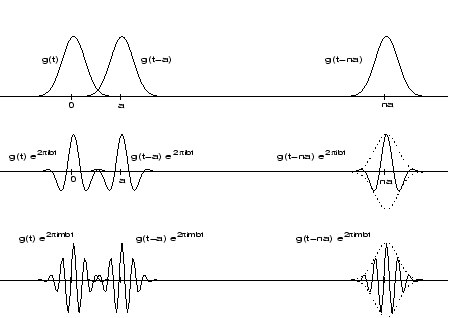
Let us take for instance a short segment of Mozart's Magic Flute (say thirty seconds and the corresponding number of samples, as they are stored on a CD). If we represent this piece of music as a function of time, we may be able to perceive the transition from one note to the next, but we get little insight about which notes are in play. On the other hand the Fourier representation may give us a clear indication about the prevailing notes in terms of the corresponding frequencies, but information about the moment of emission and duration of the notes is masked in the phases. Although both representations are mathematically correct, but one does not have to be a member of the Vienna Philharmonic Orchestra to find neither of them very satisfying. According to our hearing sensations we would intuitively prefer a representation which is local both in time and frequency, like music notation, which tells the musician which note to play at a given moment. Additionally such a local time-frequency representation should be discrete, so that it is better adapted to applications.

Dennis Gabor had similar considerations in mind, when he introduced in 1946 in his ``Theory of Communication'' a method to represent a one-dimensional signal in two dimensions, with time and frequency as coordinates [Gab46]. Gabor's research in communication theory was driven by the question how to represent locally as good as possible by a finite number of data the information of a signal which is given a priori through uncountably many function values $ f(t)$. He was strongly influenced by developments in quantum mechanics, in particular by Heisenberg's uncertainty principle and by the fundamental results of Nyquist and Hartley. on the limits for the transmission of information over a channel.

Gabor proposed to expand a function $ f$ into a series of elementary functions, which are constructed from a single building block by translation and modulation (i.e. translation in the frequency domain). More precisely he suggested to represent $ f$ by the series

$\displaystyle f(t) = \sum_{n,m \in \Z} c_{m,n} g_{m,n}(t) \,.$ (1)

where the elementary functions $ g_{m,n}$ are given by

$\displaystyle g_{m,n}(t) = g(t-n a) e^{2\pi i m b t}, \quad m,n \in \Z$ (2)

for a fixed function $ g$ and time-frequency shift parameters $ a,b >0$. A typical set of Gabor elementary functions is illustrated in Figure 1.

Figure 1: Gabor's elementary functions $ g_{m,n}(t) = g(t-na) e^{2\pi i mbt}$ are shifted and modulated copies of a single building block $ g$ ($ a$ and $ b$ denoting the time shift and the frequency shift parameter, respectively). Each $ g_{m,n}$ has an envelope of the shape of $ g$ (only the real part of the functions $ g_{m,n}$ is shown).
\begin{figure}\begin{center} \epsfig{file=gabframe.eps,width=100mm,height=70mm}\end{center}\end{figure}

We could also say that the $ g_{m,n}$ in (0.2) are obtained by shifting $ g$ along a lattice $ \Lambda = a\Z \times b\Z$ in the time-frequency plane. If $ g$ and its Fourier transform $ {\hat g}$ are essentially localized at the origin, then $ g_{m,n}$ is essentially localized at $ (na,mb)$ in the time-frequency plane. Hence each such elementary function $ g_{m,n}$ essentially occupies a certain area (``logon'') in the time-frequency plane. Each of the expansion coefficients $ c_{m,n}$, associated to a certain area of the time-frequency plane via $ g_{m,n}$, represents one quantum of information. For properly chosen shift parameters $ a,b$ the $ g_{m,n}$ cover the time-frequency plane, as demonstrated in Figure 2.

Figure 2: If $ g$ is localized at the origin in the time-frequency plane, then $ g_{m,n}$ is localized at the point $ (na,mb)$. For appropriate lattice constants $ a,b$ the $ g_{m,n}$ cover the whole time-frequency plane.
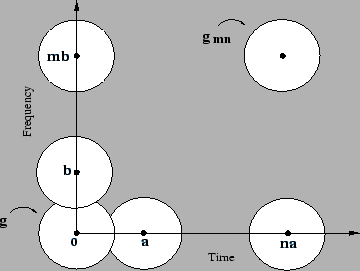
\begin{figure}\begin{center} \epsfig{file=gabcov.ps,width=80mm,height=60mm}\end{center}\end{figure}

Gabor proposed to use the Gauss function and its translations and modulations with shift parameters $ ab=1$ as elementary signals, since they ``assure the best utilization of the information area in the sense that they possess the smallest product of effective duration by effective width'' [Gab46]. Recall that the uncertainty principle inequality states that for all functions $ f \in \Ltsp(\R)$ and for all points $ (t_0,\omega_0)$ in the time-frequency plane

$\displaystyle \Vert f\Vert^2_2 \le 4 \pi \Vert(t-t_0) f(t)\Vert _2 \Vert(\omega-\omega_0) \hat{f}(\omega)\Vert _2$    

where equality is achieved only by functions of the form

$\displaystyle g(t) = C e^{2\pi i t \omega_0} e^{-s(t-t_0)^2}\,, \quad C \in \C, \, s >0,$ (3)

i.e., by modulated and translated Gaussians. The Fourier transform of the Gauss function is of the same analytic form, its sharpness is reciprocal.

It is obvious that time series and Fourier series are limiting cases of Gabor's series expansion. The first one may be obtained by letting $ s \rightarrow 0$ in (0.3), in which case the $ g_{m,n}$ approximate the delta distribution $ \delta$, in the second case, the $ g_{m,n}$ become ordinary sine and cosine waves for $ s \rightarrow \infty$.

The idea to represent a function $ f$ in terms of the time-frequency shifts of a single atom $ g$ did not only originate in communication theory but somewhat 15 years earlier also in quantum mechanics. In an attempt to expand general functions (quantum mechanical states) with respect to states with minimal uncertainty, John von Neumann [vN55] introduced in 1932 a set of coherent states on a lattice with lattice constants $ ab=h$ in the phase space with position and momentum as coordinates (here $ h$ is the Planck constant). These states, associated with the Weyl-Heisenberg group are in principle the same used by Gabor. Therefore the system $ \{g_{m,n}\}$ is also called Weyl-Heisenberg system, and the time-frequency lattice with lattice constants $ ab=1$ is also referred to as von Neumann lattice. We recommend the book of Klauder and Skagerstam for an excellent review on coherent states [KS85].

Only two years after Gabor's paper, Shannon published ``A Mathematical Theory of Communication'' [Sha48]. It should be emphasized that the temporal coincidence is not the only connection between Gabor theory and Shannon's principles of information theory. Both, Shannon and Gabor, tried to ``cover'' the time-frequency plane with a set of functions, transmission signals for digital communication in Shannon's case and building blocks for natural signals in Gabor's case. While Gabor explicitly suggested the Gaussian function and Weyl-Heisenberg structure, Shannon only emphasized the relevance of orthonormal bases without explicitly suggesting a signal set design. Yet, the determination of a critical density (referred to as degrees of freedom per time and bandwidth in Shannon's work) was one of the key mathematical prerequisites for Shannon's famous Capacity Theorem. In summary, both Gabor and Shannon worked about the same time on communication engineering problems related to Heisenberg uncertainty and phase space density, where at that time only very few mathematicians, most prominently von Neumann, had touched upon their basics. Note, however, that Shannon's work certainly had a greater impact on the engineering community than the work of Gabor.

Two questions arise immediately with an expansion of the form (0.6):

While Gabor was awarded the Nobel Prize in Physics in 1971 for the conception of holography, his paper on ``Theory of Communication'' went almost unnoticed until the early 80's, when the work of Bastiaans and Janssen refreshed the interest of mathematicians and engineers in Gabor analysis. The connection to wavelet theory1 and the increasing interest of scientists in signal analysis and frame theory was then very much influenced by the work of I. Daubechies. But before we proceed to the 80's let us go back to the 30's and 40's and follow the development of Gabor theory from the signal analysis point of view.