Local time-frequency analysis and short time Fourier transform

Time-frequency analysis plays a central role in signal analysis. Already long ago it has been recognized that a global Fourier transform of a long time signal is of little practical value to analyze the frequency spectrum of a signal. High frequency bursts for instance cannot be read off easily from $ \hat{f}$. Transient signals, which are evolving in time in an unpredictable way (like a speech signal or an EEG signal) necessitate the notion of frequency analysis that is local in time.

In 1932, Wigner derived a distribution over the phase space in quantum mechanics [Wig32]. It is a well-known fact that the Wigner distribution of an $ \Ltsp$-function $ f$ is the Weyl symbol of the orthogonal projection operator onto $ f$ [Fol89]. Some 15 years later, Ville, searching for an ``instantaneous spectrum'' - influenced by the work of Gabor - introduced the same transform in signal analysis [Vil48]. Unfortunately the non-linearity of the Wigner distribution causes many interference phenomena, which makes it less attractive for many practical purposes [Coh95].

A different approach to obtain a local time-frequency analysis (suggested by various scientists, among them Ville), is to cut the signal first into slices, followed by doing a Fourier analysis on these slices. But the functions obtained by this crude segmentation are not periodic, which will be reflected in large Fourier coefficients at high frequencies, since the Fourier transform will interpret this jump at the boundaries as a discontinuity or an abrupt variation of the signal. 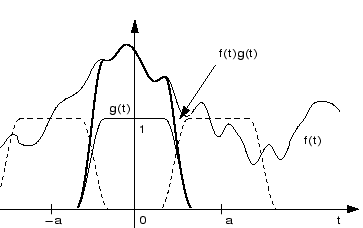To avoid these artifacts, the concept of windowing has been introduced. Instead of localizing $ f$ by means of a rectangle function, one uses a smooth window-function for the segmentation, which is close to $ 1$ near the origin and decays towards zero at the edges. Popular windows which have been proposed for this purpose are associated with the names Hamming, Hanning, Bartlett, or Kaiser. If the window is in $ \Csp^{\infty}$ (i.e. infinitely differentiable) one finds that for any $ \Csp^{\infty}$-function $ f$ the localized Fourier coefficients show at least polynomial decay in the frequency direction.

Figure 3: For fixed $ t_0$ the short time Fourier transform of a function $ f(t)$ describes the local spectral content of $ f(t)$ near $ t_0$, as a function of $ \omega $. It is defined as the Fourier transform of $ f(t)g(t-t_0)$, where $ g(t)$ is a (often compactly supported) window function, localized around the origin. Moving the center of the window $ g$ along the real line, allows to obtain ``snapshots'' of the time-frequency behavior of $ f$. We depict a collection of such shifted windows, with $ t_0 = -a, 0, a$.
\begin{figure}\begin{center} \epsfig{file=stftplot.eps,width=80mm,height=50mm}\end{center}\end{figure}

The resulting local time-frequency analysis procedure is referred to as (continuous) short time Fourier transform or windowed Fourier transform. It is schematically represented in Figure 3. In mathematical notation, the short time Fourier transform (STFT) of an arbitrary function $ f \in \LtR$ with respect to a given (often compactly supported) window $ g$ is defined as

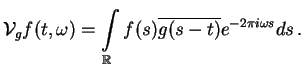$\displaystyle {\cal V}_{g}f(t,\omega) = \int \limits_{\R} f(s) \overline{g(s - t)} e^{-2\pi i \omega s} ds \,.$    

The function $ f$ can be recovered from its STFT via the inversion formula

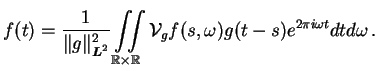$\displaystyle f(t) = \frac{1}{\Vert g\Vert^2_\Ltsp}\iint \limits_{\R \times \R} {\cal V}_{g}f(s,\omega) g(t-s) e^{2\pi i \omega t} dt d\omega \,.$    

It is possible to derive the inversion formula (the integral is understood in the mean square sense) from the following formula, which itself can be seen as an immediate consequence of Moyal's formula. In particular it implies that for a normalized window $ g$ satisfying $ \Vert g \Vert _2 = 1$ the mapping $ f \mapsto {\cal V}_{g}f$ is an isometric embedding from $ \LtR$ into $ \Ltsp(\Rst^{2d})$

$\displaystyle \Vert{\cal V}_{g}f\Vert _{\Ltsp(\R \times \R)} = \Vert g\Vert _{\Ltsp (\R)} \Vert f\Vert _{\Ltsp(\R)}\,.$    

The STFT and the spectrogram $ \vert{\cal V}_{g}f(t,\omega)\vert^2$ have become standard tools in signal analysis. However the STFT has also its disadvantages, such as the limit in its time-frequency resolution capability, which is due to the uncertainty principle. Low frequencies can be hardly depicted with short windows, whereas short pulses can only poorly be localized in time with long windows, see also Figure 4 for an illustration of this fact. These limitations in the resolution were one of the reasons for the invention of wavelet theory.

Figure 4: A signal, its Fourier transform and short time Fourier transforms with windows of different duration. (a) The signal itself consists of a constant sine wave (with 35 Hz), a quadratic chirp (starting at time 0 with 25 Hz and ending after one second at 140 Hz) and a short pulse (appearing after 0.3 sec.). (b) Using a wide window for the STFT leads to good frequency resolution. The constant frequency term can be clearly seen, also the quadratic chirp. However the short pulse is hardly visible. (c) Using a narrow window gives good time resolution, clearly localizing the short pulse at 0.3 sec., but the information about the constant harmonic gets very unsharp. (d) In this situation a window of medium width yields a satisfactory resolution both in time and frequency.
\begin{figure}\begin{center} \subfigure[Signal and its Fourier transform]{ \epsf... ...ow]{ \epsfig{file=win_opt.eps,width=50mm,height=50mm}} \end{center}\end{figure}

Another disadvantage for many practical purposes is the high redundancy of the STFT. This fact suggests to ask, if we can reduce this redundancy by sampling $ {\cal V}_{g}f(t,\omega)$. The natural discretization for $ t,\omega$ is $ t = n a, \omega = m b$ where $ a,b >0$ are fixed, and $ n,m$ range over $ \Z$, i.e., to sample $ {\cal V}_{g}f$ over a time-frequence lattice of the form $ a \Z \times b \Z $.

Large values of $ a,b$ give a coarse discretization, whereas small values of $ a,b$ lead to a dense sampled STFT.

Using the operator notation $ T_t$ and $ M_\omega$ for translation and modulation, respectively, we can express the STFT of $ f$ with respect to a given window $ g$ as

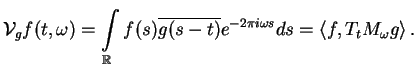$\displaystyle {\cal V}_{g} f (t,\omega) = \int \limits_{\R} f(s) \overline{g(s - t)} e^{-2\pi i \omega s} ds = \langle f, T_t M_{\omega} g \rangle \,.$    

Hence the sampled STFT of a function $ f$ can also be interpreted as the set of inner products of $ f$ with the members of the family $ \{g_{m,n}\} = \{T_{na} M_{mb} g\}$ with discrete labels in the lattice $ a \Z \times b \Z $. It is obvious that the members of this family are constructed in the same way as the representation functions $ g_{m,n}$ in Gabor's series expansion. Thus the sampled STFT is also referred to as Gabor transform.

0 Thus the linear mapping

$\displaystyle f \mapsto \{\langle f, g_{m,n}\rangle\}_{m,n \in \Z}$   where$\displaystyle \,\,\, g_{m,n}= T_{na} M_{mb} g,\, \,\, \,a,b > 0,$ (4)

is also referred to as Gabor transform or Gabor analysis mapping, in analogy to the Gabor synthesis mapping defined in (0.6).

Two questions arise immediately with the discretization of the STFT

Recall, that in connection with the Gabor expansion of a function we have asked

It turns out that the question of recovering $ f$ from the samples (at lattice points) of its STFT with respect to the window $ g$ is actually dual to the problem of finding coefficients for the Gabor expansion of $ f$ with atom $ g$, using the same lattice to generate the time-frequency shifts of $ g$. Both problems can be successfully and mathematically rigorously attacked using the concept of frames and surprisingly for both questions the same ``dual'' Gabor atom has to be used.