Critical sampling, oversampling, and the Balian-Low Theorem

We have mentioned earlier that Gabor suggested to use the Gaussian function as atom $ g$, since it minimizes the uncertainty principle inequality. Recalling that the $ g_{m,n}= T_{na} M_{mb} g$ are the coherent states associated to the Weyl-Heisenberg group in quantum mechanics, we remind that this choice corresponds to the canonical coherent states.

Exploiting the link between Gaussian coherent states and the Bargmann space of entire functions it was proved in 1971 by Peremolov [Per71] and independently by Bargmann et al. [BBGK71] that the canonical coherent states $ g_{m,n}$ are complete in $ \Ltsp(\R)$ if and only if $ ab \le 1$. Bacry, Grossmann and Zak [BGZ75] showed in 1975 that if $ ab=1$, then

$\displaystyle \underset{f \in \Ltsp(\R)}{\inf} \sum_{m,n} \vert\langle f,g_{m,n}\rangle \vert^2=0$ (12)

although the $ g_{m,n}$ are complete in $ \Ltsp(\R)$. Formula (0.10) implies that for Gabor's original choice of the Gaussian and $ ab=1$, the set $ \{g_{m,n}\}$ is not a frame for $ \Ltsp(\R)$. Thus there is no numerically stable algorithm to reconstruct $ f$ from the $ \langle f, g_{m,n}\rangle$.

Bastiaans was the first who has published an analytic solution to compute the Gabor expansion coefficients for the case $ a=b=1$ and $ g$ equal the Gaussian. He constructed a function $ \gamma$, such that

$\displaystyle f = \sum_{m,n} \langle f, g_{m,n}\rangle \gamma_{m,n}$ (13)

with $ \gamma_{m,n}= T_{na} M_{mb} \gamma $. Note however that (0.11) does not even converge in a weak $ \Ltsp$-sense, in fact $ \gamma$ is not in $ \Ltsp$, as was pointed out by Janssen [Jan81]. He showed that convergence holds only in the sense of distributions.

Using entire function methods, Lyubarskii and independently Seip and Wallsten showed that for the Gaussian $ g$ the family $ \{g_{m,n}\}$ is a frame whenever $ ab <1$. According to Janssen the dual function $ \gamma$ is then even a Schwartz function.

As a corollary of deep results on $ C^*$-algebras by Rieffel it was proved that the set $ \{g_{m,n}\}$ is incomplete in $ \LtR$ for any $ g \in \LtR$, if $ ab >1$. This fact can be seen as a Nyquist criterion for Gabor systems. The non-constructive proof makes use of the properties of the von Neumann algebras, generated by the operators $ T_{na} M_{mb}$. Daubechies [Dau90] derived this result for the special case of rational $ ab$. Janssen showed that the $ g_{m,n}$ cannot establish a frame for any $ g \in \LtR$, if $ ab >1$ without any restriction on $ ab$. One year earlier Landau proved the weaker result that $ \{g_{m,n}\}$ cannot be a frame for $ \LtR$ if $ ab >1$ and both $ g$ and $ \hat{g}$ satisfy certain decay conditions [Lan93]. On the other hand his result includes the case of irregular Gabor systems, where the sampling set is not necessarily a lattice in $ \Rst \times \Rst$.

All these results remind on the role of the Nyquist density for sampling and reconstruction of bandlimited functions in Shannon's Sampling Theorem. Hence it is natural to classify Gabor systems according to the corresponding sampling density of the time-frequency lattice:

The case $ ab=1$ is also distinguished among all others by the fact, that the time-frequency shift operators, which are used to build the coherent frame, commute with each other (without non-trivial factor).

Clearly there exist many choices for $ g$, so that $ \{g_{m,n}\}$ is a frame or even an orthonormal basis (ONB) for $ \LtR$. Two well-known examples of functions for which the family $ \{T_{na} M_{mb} g\}$ constitutes an ONB are the rectangle function (which is 1 for $ 0 \le t \le 1$ and zero else), and the sinc-function $ g(t) = \sin \pi t/\pi t$. However in the first case $ \int \omega^2 \vert\hat{g}(\omega)\vert^2 = \infty$, in the second case $ \int t^2 \vert g(t)\vert^2 = \infty$. Thus these choices lead to systems with bad localization properties in either time or frequency. Even if we drop the orthogonality requirement, we cannot construct Riesz bases with good time-frequency localization properties for the limit case $ ab=1$. This is the contents of the celebrated Balian-Low Theorem [Bal81,Low85], which describes one of the key facts in Gabor analysis:


Balian-Low Theorem: If the $ g_{m,n}$ constitute a Riesz basis for $ \LtR$, then

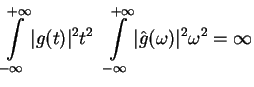$\displaystyle \int \limits_{-\infty}^{+\infty} \vert g(t)\vert^2 t^2 \enspace \int \limits_{-\infty}^{+\infty} \vert{\hat g}(\omega)\vert^2 \omega^2 = \infty$    

According to Gabor's heuristics the integer lattice in the time-frequency plane was chosen to make the choice of coefficients ``as unique as possible'' (unfortunately one cannot have strict uniqueness since there are bounded sequences which represent the zero-function in a non-trivial, but only distributional way). In focusing his attention on this uniqueness problem he apparently overlooked that the use of well-localized building blocks to obtain an expansion $ f = \sum_{m,n} c_{m,n} g_{m,n}$ does not imply that the computation of the coefficient $ c_{m,n}$ can be carried out by a ``local'' procedure, using only information localized around the point $ (an,bm)$ in the time-frequency plane. The problem of lack of time-frequency locality of the Gabor coefficients is not only severe in the critical case, but becomes more and more serious as one uses a sequence of lattices which are close-to-critical sampling. This fact becomes clear by observing that the corresponding dual functions lose their time-frequency localization, see also Figure 5.

It appears that Gabor families having some (modest) redundancy, which allows to have a pair of dual Gabor atoms $ (g,\gamma)$ where each function of this dual pair is well localized in time and frequency (cf. also Figure 5), are more appropriate as a tool in Gabor's original sense. Clearly under such premises one has to give up the uniqueness of coefficients and even the uniqueness of $ \gamma$. The choice $ \gamma = S^{-1} g$ is in some sense canonical and - as we have seen above - appropriate Gabor coefficients can be easily determined as samples of the STFT with window $ \gamma$.

Figure 5: Dual Gabor functions for different oversampling rates. The dual window approaches Bastiaan's dual function for critical sampling and approximates the given Gabor window $ g$ with increasing oversampling rate.
\begin{figure}\begin{center} \subfigure[Gabor function $g$]{ \epsfig{file=gabato... ...]{ \epsfig{file=gabred240.eps,width=45mm,height=40mm}} \end{center}\end{figure}

Is there no way to obtain an orthonormal basis for $ \LtR$ with good time-frequency properties based on Gabor's approach?

Wilson observed that for the study of the kinetic operator in quantum mechanics, one does not need basis functions that distinguish between positive and negative frequencies of the same order. Musicians probably would also agree to such a relaxation of requirements. Thus we are looking for complete orthonormal systems which are essential of Weyl-Heisenberg type, but allowing to have linear combinations of $ g_{t,s}$ with $ g_{t,-s}$. It turns out that by this seemingly small modification a family of orthonormal bases for $ \Ltsp(\R)$ can be constructed, the so-called Wilson bases, avoiding the Balian-Low phenomenon. Wilson's suggestion was turned into a construction by Daubechies, Jaffard and Journé, who gave a recipe how to obtain such an orthonormal Wilson basis from a tight Gabor frame for $ a = 1/2$ and $ b =1$.

A general construction that includes many examples of Wilson bases as well as wavelet bases are the local trigonometric bases of Coifman and Meyer.