Applications

Gabor systems are applied in numerous engineering applications, many of them without obvious connection to the traditional field of time-frequency analysis for deterministic signals.

Any countable set of test functions $ \{f_n\}$ in a Hilbert space conveys a linear mapping between function spaces and sequence spaces. In one direction scalar products $ \langle f, f_n \rangle $ are taken (analysis mapping), and in the other direction the members $ c = \{c_n\}$ from the sequence space are used as coefficient sequences in a series of the form $ \sum_n c_n f_n $ (synthesis mapping). In our concrete context the analysis mapping is given by the Gabor transform (0.5) (i.e., the sampled short time Fourier transform) and the synthesis mapping is given by the Gabor expansion (0.6). In principle there exists two basic setups for the use of Gabor systems, which pervade most applications:

Figure: Digital communication systems transmit sequences of binary data over a continuous time physical channel. The transmitter sends a signal, formed by linear combination of the $ g_{m,n}$, weighted by the binary coefficients $ c_{m,n}$ (=Gabor synthesis). The receiver recovers the coefficients by computing inner products with the corresponding analysis functions

Figure: Schematic representation of Gabor setup for signal denoising or compression. The coefficients (computed by Gabor transform) are subject to linear or nonlinear (such as thresholding or source coding) modifications. The modified (e.g., denoised or decompressed) signal is obtained by Gabor expansion.
\begin{figure}\begin{center} \epsfig{file=filt2a1.eps,width=110mm,height=45mm}\end{center}\end{figure}


Speech signal analysis:
Speech signals are one of the classical applications of linear time-frequency representations. In fact, the analysis of speech signals was the driving force that led to the invention of (a nondigital filter bank realization of) the spectrogram. The advent of the FFT made the STFT up to now to the standard tool of speech analysts.

Time-Varying Spectral Estimation:
Time-invariant spectral estimation, a standard procedure for time series analysis, is of fundamental relevance in most areas of science and technology. The basic principle is to model the time series as a realization of a stationary random process whose power spectrum can be characterized by a typically lower dimensional data set (uniformly spaced frequency samples in a nonparametric setup or, e.g., poles and zeros of an ARMA model). There exists a large variety of robust and efficient procedures for power spectrum estimation. The natural generalization of the stationary framework to nonstationary environments leads to a longstanding theoretical problem: What is the proper definition of a time-varying power spectrum of a nonstationary process? Classical definitions are Priestley's evolutionary spectrum and the Wigner-Ville spectrum which are closely related to the operator symbols of Weyl and Kohn-Nirenberg. Whether or not one trusts either definition it is clear that a time-varying power spectrum is (i) time-frequency parametrized and (ii) a quadratic form of the data, hence the magnitude-squared Gabor coefficients establish the basis of any nonparametric estimation procedure.


Representation and Identification of Linear Systems:
The theory of linear time-invariant (LTI) systems and in particular the symbolic calculus of transfer functions is a standard tool in all areas of mechanical and electrical engineering. Strict translation invariance is however almost always a pragmatical modeling assumption which establishes a more or less accurate approximation to the true physical system. Hence it is a problem of longstanding interest to generalize the transfer function concept from LTI to linear time-varying (LTV) systems. Such a time-varying transfer function was suggested by Zadeh in 1950. It is formally equivalent to the Weyl-Heisenberg operator symbol of Kohn and Nirenberg. Pseudodifferential operators are the classical way to establish a symbol classification that keeps some of the conceptual power which the Fourier transform has for LTI systems. Recently Gabor frames have turned out to be a useful tool to the analysis of pseudodifferential operators.


Digital Communication:
Digital communication systems transmit sequences of binary data over a continuous time physical channel. An ideal physical channel is bandlimited without in-band distortions. 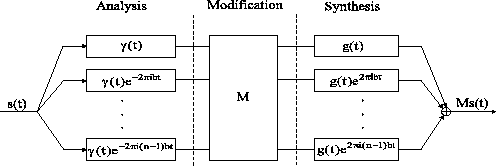Under this idealized assumption, digital communication systems can be implemented by selecting a Gabor-structured orthonormal system, transmitting a linear combination of the elementary signals, weighted by the binary coefficients (Gabor synthesis) and the receiver recovers the coefficients by computing inner products with the known basis functions (matched filter receiver = Gabor analysis), see Fig.[*]. However, in wireless communication systems which is one of the challenging research areas, the physical channel is subject to severe linear distortions and hundreds of users communicate over the same frequency band at the same time. Traditional OFDM (orthogonal frequency division multiplex) systems can be interpreted as orthonormal Gabor systems with critical sampling $ ab=1$ and come therefore with the well-known bad time-frequency localization properties of the building blocks. Since completeness is not a concern here, recent works suggest the use of a coarser grid $ ab >1$, together with good TF-localized atoms to obtain more robustness.


Image representation and biological vision:
Gabor functions were successfully applied to model the response of simple cells in the visual cortex. In our notation, each pair of adjacent cells in the visual cortex represents the real and imaginary part of one coefficient $ c_{m,n}$ corresponding to $ g_{m,n}$. Clearly the Gabor model cannot capture the variety and complexity of the visual system, but it seems to be a key in further understanding of biological vision.

Among the people who paved the way for the use of Gabor analysis in pattern recognition and computer vision one certainly has to mention Zeevi, M. Porat, and their coworkers and Daugman. Motivated by biological findings, Daugman and Zeevi and Porat proposed the use of Gabor functions for image processing applications, such as image analysis and image compression.

Since techniques from signal processing are of increasing importance in medical diagnostics, we mention a few applications of Gabor analysis in medical signal processing. The Gabor transform has been used for the analysis of brain function, such as for detection of epileptic seizures in EEG signals, study of sleep spindles. The role of the Heisenberg group in magnetic resonance imaging has been recently analyzed by Schempp.