Solving Mean Value Theorem Problems
The Mean Value Theorem is one of the most important theorems in Introductory Calculus, and it forms the basis for proofs of many results in subsequent and advanced Mathematics courses. The
history of this theorem begins in the 1300's with the Indian Mathematician
Parameshvara , and is eventually based on the academic work of Mathematicians Michel Rolle in 1691 and Augustin Louis Cauchy in 1823.
The formal statement of this theorem together with an illustration of the theorem will follow. I will also state Rolle's Theorem , which is used in the proof the Mean Value Theorem. Both theorems are given without proof, and all subsequent problems here will be referencing only the Mean Value Theorem. All functions are assumed to be real-valued.
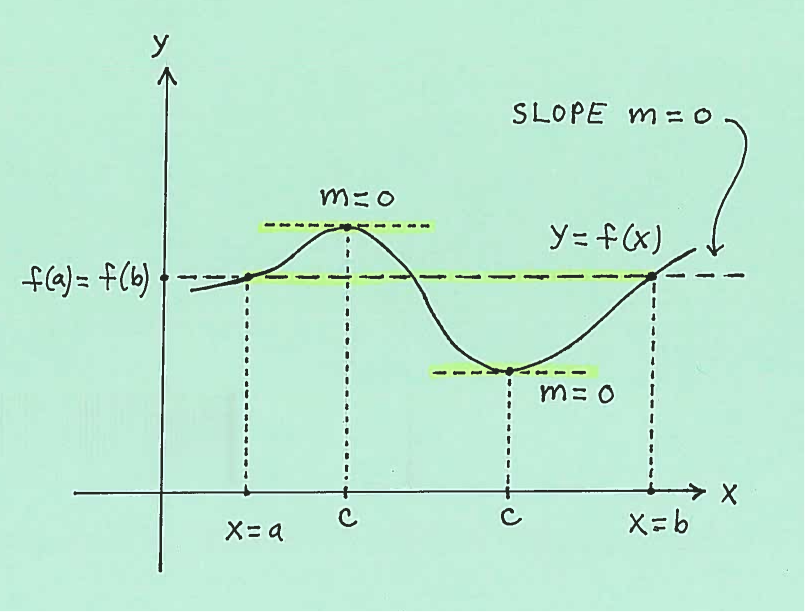
ROLLE'S THEOREM: Let $f$ be a continuous function on the closed interval $ [a, b] $ and differentiable on the open interval $ (a, b) $ with $f(a)=f(b)$. Then there is at least one number $c$ ($x$-value) in the interval $(a, b)$ which satifies
$$ f'(c)=0 $$
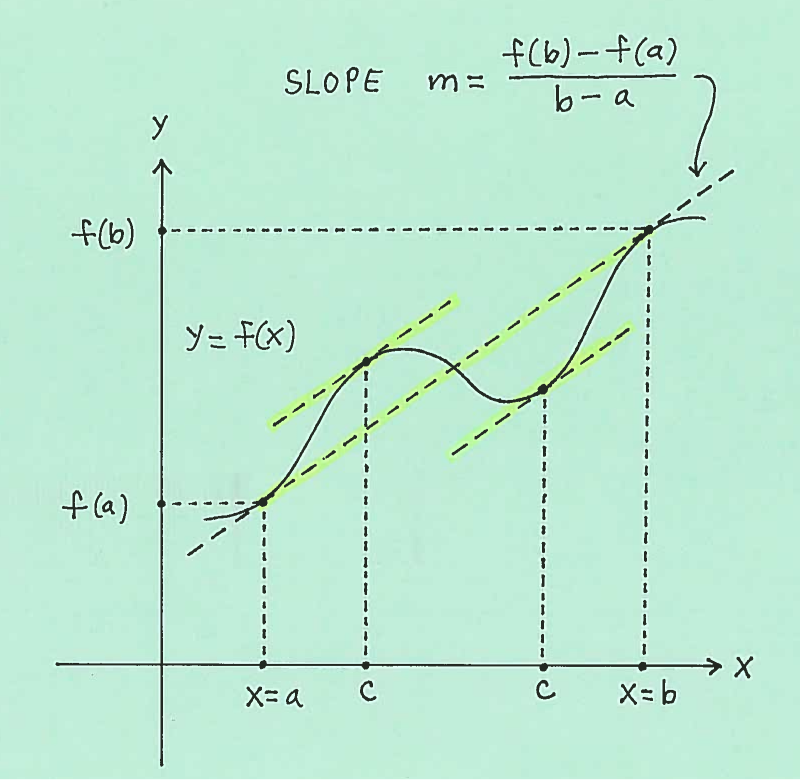
MEAN VALUE THEOREM: Let $f$ be a continuous function on the closed interval $ [a, b] $ and differentiable on the open interval $ (a, b) $. Then there is at least one number $c$ ($x$-value) in the interval $(a, b)$ which satifies
$$ f'(c)= \displaystyle{ f(b) - f(a) \over b-a } $$
Numerous proofs for Rolle's Theorem and the Mean Value Theorem can easily be found on the internet. I have attached proofs of both Theorems here , along with other results related to the Mean-Value Theorem.
In the list of Mean Value Theorem Problems which follows, most problems are average and a few are somewhat challenging.
- PROBLEM 1 : Determine if the Mean Value Theorem can be applied to the following function on the the given closed interval. If so, find all possible values of $c$: $ \ f(x)=3+ \sqrt{x} \ $ on $ \ [0, 4] $
Click HERE to see a detailed solution to problem 1.
- PROBLEM 2 : Determine if the Mean Value Theorem can be applied to the following function on the the given closed interval. If so, find all possible values of $c$: $ \ f(x)= x^2(x-1) \ $ on $ \ [0, 3] $
Click HERE to see a detailed solution to problem 2.
- PROBLEM 3 : Determine if the Mean Value Theorem can be applied to the following function on the the given closed interval. If so, find all possible values of $c$: $ \ f(x)= x^2-x^{2/3} \ $ on $ \ [-1, 8] $
Click HERE to see a detailed solution to problem 3.
- PROBLEM 4 : Determine if the Mean Value Theorem can be applied to the following function on the the given closed interval. If so, find all possible values of $c$: $ \ f(x)= \displaystyle{ x \over 1+x} \ $ on $ \ [1, 3] $
Click HERE to see a detailed solution to problem 4.
- PROBLEM 5 : Determine if the Mean Value Theorem can be applied to the following function on the the given closed interval. If so, find all possible values of $c$: $ \ f(x)= \sin 2x \ $ on $ \ [0, \pi] $
Click HERE to see a detailed solution to problem 5.
- PROBLEM 6 : Determine if the Mean Value Theorem can be applied to the following function on the the given closed interval. If so, find all possible values of $c$: $ \ f(x)= x + 3\cos x \ $ on $ \ [-\pi, \pi] $
Click HERE to see a detailed solution to problem 6.
- PROBLEM 7 : Determine if the Mean Value Theorem can be applied to the following function on the the given closed interval. If so, find all possible values of $c$: $ \ f(x)= 2x + \sqrt{x-1} \ $ on $ \ [1, 5] $
Click HERE to see a detailed solution to problem 7.
- PROBLEM 8 : Determine if the Mean Value Theorem can be applied to the following function on the the given closed interval. If so, find all possible values of $c$: $ \ f(x)= x^3+x \ $ on $ \ [-1, 0] $
Click HERE to see a detailed solution to problem 8.
- PROBLEM 9 : Determine if the Mean Value Theorem can be applied to the following function on the the given closed interval. If so, find all possible values of $c$: $ \ f(x)= \displaystyle{ x^3 \over 1 - \sqrt{x} } \ $ on $ \ [0, 4] $
Click HERE to see a detailed solution to problem 9.
- PROBLEM 10 : Determine if the Mean Value Theorem can be applied to the following function on the the given closed interval. If so, find all possible values of $c$: $ \ f(x)= (8-x)^{1/3} \ $ on $ \ [0, 8] $
Click HERE to see a detailed solution to problem 10.
- PROBLEM 11 : Let $ s(t) $ be the total miles that you have driven on your trip down a toll road freeway after time $t$ hours. Assume also that $ s(1/3)=10 \ miles $ and $ s(1.2)= 82 \ miles $. At a checkpoint along the toll road you admit these facts to a highway patrol officer, who is familiar with the Mean Value Theorem. The officer makes a few quick calculations, smiles, then politely prepares to write you a traffic ticket. Explain why.
Click HERE to see a detailed solution to problem 11.
- PROBLEM 12 : Use the Mean Value Theorem to show that
$ \ \ \Big| \sin w - \sin z \Big| \le \Big| w-z \Big| \ \ $ for $ \ 0 \le z < w \le 2 \pi $ .
Click HERE to see a detailed solution to problem 12.
- PROBLEM 13 : Use the Mean Value Theorem to show that
$ \ \ \Big| \tan w - \tan z \Big| \le 2 \Big| w-z \Big| \ \ $ for $ \ 0 \le z < w \le \pi/4 $ .
Click HERE to see a detailed solution to problem 13.
- PROBLEM 14 : Use the Mean Value Theorem to show that
$ \ \ \Big| \ln w - \ln z \Big| \le 3 \Big| w-z \Big| \ \ $ for $ \ 1/3 \le z < w \le 3 $ .
Click HERE to see a detailed solution to problem 14.
Click HERE to return to the original list of various types of calculus problems.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by
clicking on the following address :
kouba@math.ucdavis.edu
A heartfelt "Thank you" goes to The MathJax Consortium for making the construction of this webpage fun and easy.
Duane Kouba ...
September 20, 2020


