The Proof Page
by D. A. Kouba
Section 1.2- Conditionals and Biconditionals; Mathematically Equivalent Statements
In this section we will introduce two more mathematical connectives. This will allow for a wider and more useful range of propositional forms. In particular, we will now include in our propositional forms, sentences of the form ``If  , then
, then  ", one of the most useful forms in the study of mathematics.
", one of the most useful forms in the study of mathematics.
 : Let
: Let  and
and  be propositions. The
be propositions. The

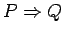 (read ``
(read `` implies
implies  ." or ``If
." or ``If  , then
, then  .") is true whenever
.") is true whenever  is true or
is true or  is false.
is false.
The following truth table illustrates all possible truth values for the conditional sentence
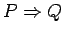 .
.
 : Let
: Let  and
and  be propositions. The
be propositions. The
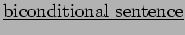
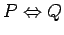 (read ``
(read `` if and only if
if and only if  .") is true exactly when
.") is true exactly when  and
and  have the same truth values.
have the same truth values.
The following truth table illustrates all possible truth values for the biconditional sentence
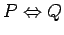 .
.
 : Let
: Let  and
and  be propositions.
be propositions.
- 1.) The
 of
of
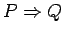 is
is
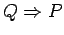 .
.
- 2.) The
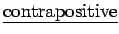 of
of
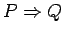 is
is
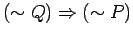 .
.
The following two theorems present a list of equivalent propositions. These equivalences will allow us to easily change from one propositional form to another.
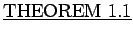 : Let
: Let  and
and  be propositions.
be propositions.
- a.)
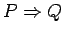 is equivalent to
is equivalent to
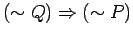 .
.
- b.)
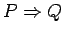 is NOT equivalent to
is NOT equivalent to
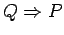 .
.
 :
:
 : Equivalence of the following statements follows from Theorem 1.1 a.).
: Equivalence of the following statements follows from Theorem 1.1 a.).
- 1.) If a function is differentiable at
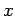 , then the function is continuous at
, then the function is continuous at 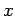 .
.
- 2.) If a function is not continuous at
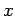 , then the function is not differentiable at
, then the function is not differentiable at 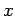 .
.
 : The following statements are not equivalent. See Theorem 1.1 b.).
: The following statements are not equivalent. See Theorem 1.1 b.).
- 1.) If I go to Mexico and lay on the beach, then I will get a suntan.
- 2.) If I have a suntan, then I went to Mexico and laid on the beach.
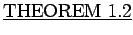 : Let
: Let 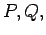 and
and 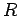 be propositions.
be propositions.
- a.)
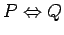 is equivalent to
is equivalent to
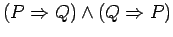 .
.
- b.)
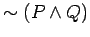 is equivalent to
is equivalent to
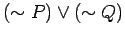 .
.
- c.)
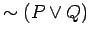 is equivalent to
is equivalent to
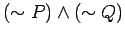 .
.
- d.)
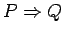 is equivalent to
is equivalent to
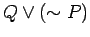 .
.
- e.)
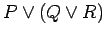 is equivalent to
is equivalent to
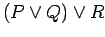 .
.
- f.)
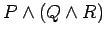 is equivalent to
is equivalent to
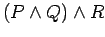 .
.
- g.)
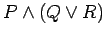 is equivalent to
is equivalent to
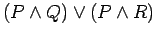 .
.
- h.)
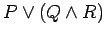 is equivalent to
is equivalent to
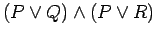 .
.
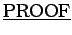 : All are easily proven using truth tables.
: All are easily proven using truth tables.
 : Parts a.) and b.) in Theorem 1.2 make the connection between ``and" and ``or" statements. Part d.) makes the connection between ``if, then" and ``or" statements. Parts e.) and f.) represent associative properties for ``and" and ``or" statements. Parts g.) and h.) illustrate distributive properties.
: Parts a.) and b.) in Theorem 1.2 make the connection between ``and" and ``or" statements. Part d.) makes the connection between ``if, then" and ``or" statements. Parts e.) and f.) represent associative properties for ``and" and ``or" statements. Parts g.) and h.) illustrate distributive properties.
Because the English language and use of common words can sometimes be ambiguous, we make the following mention of equivalent statements.
 : On The Proof Page we will assume that the statement
: On The Proof Page we will assume that the statement
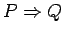 (If
(If  , then
, then  ) is equivalent to EACH of the following statements.
) is equivalent to EACH of the following statements.
- 1.)
 if
if  .
.
- 2.)
 only if
only if  .
.
- 3.)
 only when
only when  .
.
- 4.)
 whenever
whenever  .
.
- 5.)
 when
when  .
.
- 6.)
 implies
implies  .
.
- 7.)
 is sufficient for
is sufficient for  .
.
- 8.)
 is necessary for
is necessary for  .
.
 : The following sets of statements are equivalent.
: The following sets of statements are equivalent.
- 1.) . . . . . . . a.) He will get wet if he stands in the rain.
. . . . . . . . . . . . . . b.) If he stands in the rain, then he will get wet.
- 2.) . . . . . . . a.) I will get a ticket for speeding only if I get caught.
. . . . . . . . . . . . . . b.) If I get a ticket for speeding, then I got caught.
- 3.) . . . . . . . a.) She takes a bike ride whenever she is upset.
. . . . . . . . . . . . . . b.) If she is upset, then she takes a bike ride.
- 4.) . . . . . . . a.) If you get eight hours of sleep, then you will feel good in the morning.
. . . . . . . . . . . . . . b.) Feeling good in the morning is necessary for getting eight hours of sleep.
. . . . . . . . . . . . . . . . . . c.) Getting eight hours of sleep is sufficient for feeling good in the morning.
 : On The Proof Page we will assume that the statement
: On The Proof Page we will assume that the statement
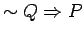 (If not
(If not  , then
, then  ) is equivalent to EACH of the following statements.
) is equivalent to EACH of the following statements.
- 1.)
 unless
unless  .
.
-
2.)
 without
without  .
.
 : The following four statements are equivalent.
: The following four statements are equivalent.
- 1.) . . . . She will not go swimming unless the water is very warm.
- 2.) . . . . She will not go swimming without the water being very warm.
- 3.) . . . . If the water is not very warm, then she will not go swimming.
- 4.) . . . . If she goes swimming, then the water is very warm. (See Theorem 1.1 a.)
 : Rewrite each of the following sentences in symbolic propositional form. Then write each sentence in conditional (If ..., then ...) form. Find solutions HERE .
: Rewrite each of the following sentences in symbolic propositional form. Then write each sentence in conditional (If ..., then ...) form. Find solutions HERE .
- 1.) It will rain or it will not hail.
- 2.) The food is cold or the food is bad.
- 3.) She is not tall or she does not have brown eyes.
- 4.) I will buy a new car only if I win the lottery.
- 5.) He will fail the biochemistry exam unless he studies all week.
- 6.) Tarzan will be very unhappy without Jane in his life.
- 7.) She won't go to the movie unless he goes with her.
- 8.) It is not true that milk is blue and bananas are red.
- 9.) You will get an A only if you study.
- 10.) You will get an A whenever you study.
- 11.) You will get an A if you study.
- l2.) To get an A it is sufficient that you study.
- l3.) To get an A it is necessary that you study.
 : Rewrite each of the following sentences in symbolic propositional form. Then use a truth table to prove that they are equivalent. Find solutions HERE .
: Rewrite each of the following sentences in symbolic propositional form. Then use a truth table to prove that they are equivalent. Find solutions HERE .
- Sentence 1 : If wealth implies happiness, then you are materialistic.
- Sentence 2 : You are wealthy and not happy, or you are materialistic.
NOTE : (ORDER OF OPERATIONS) If parantheses are not used to clearly indicate the use of connectives, then invoke the connectives in the following order- 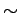 ,
, 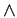 ,
, 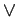 ,
, 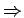 ,
,
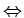 . For example,
. For example,
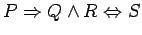 is equivalent to
is equivalent to
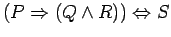 .
.
 : Provide parantheses to clarify the following ambiguous expressions. Find solutions HERE .
: Provide parantheses to clarify the following ambiguous expressions. Find solutions HERE .
RETURN to The Proof Page .
Please e-mail your comments, questions, or suggestions to D. A. Kouba at
kouba@math.ucdavis.edu .
Next: About this document ...
Duane Kouba
2002-05-11