What is an optimal transport path?

• My talk on "introduction to optimal transport paths". For readers not familar with the subject, here is the formal definition of  transport paths as well as a family of transport cost M_{alpha} defined on them.
• Answers from pure math.
• An optimal transport path between two probability measure is a geodesic in the metric space of probabilty measures ([7, theorem 5.1] and [2, section 4]), where the metric on the space of probabilty measures is the intrinsic metric induced by a nearmetric defined on the space of transport plans ([2, section 4]). Here, a nearmetric space is a generalized metric space in which the distance satisfies a relaxed triangle inequality d(x,y)<=c(d(x,z)+d(y,z)) for some constant c no less than 1. See [2] for details.
• An optimal transport path between two probability measure is a solution to the Plateau's problem: Given a "boundary curve C" ( which is the difference of two probability measures here), find a surface S (which is a rectifiable 1-current here) with boundary C of the least "surface area" ( which is the M_{alpha} cost here).   So, an optimal transport path can be viewed as a special kind of one dimensional "minimal surface".
• Answers from applied math.
• An optimal transport path is an efficient transport system for transporting given sources to given targets.

Why do we study optimal transport paths?
The study of optimal transport paths is motivated by many questions. For instance:

• Motivations from applied math.
• Describe a general phenomena that it is more cost efficient to transport items in a group than transport them individually.
• Understand the language of the nature: why many living and nonliving systems prefer to adopt "branched" transport systems? What is the role of "optimization" played in the formation of many fractal typed systems in nature? 
• Motivations from pure math.
• A geodesic between two points in the plane is a segment. Is there a geodesic from two points to three points?  Or, given two probabilty measures, what is a geodesics (if any) between them? 
• Soap films motivates the study of minimal surfaces.  What may the other "optimal" objects (e.g. trees, leaves, etc) in nature lead to? Why do they prefer "branching structures"?
• We know that a metric on a metric space may induce an intrinsic metric. The triangle inequality is assumed to play an important role there. When a distance does not satisfy the triangle inequality (or only satisfies a relaxed triangle inequality), will it still be able to induce an intrinsic metric?  If so, what does the intrinsic metric look like?

Numerical simmulation of optimal transport paths

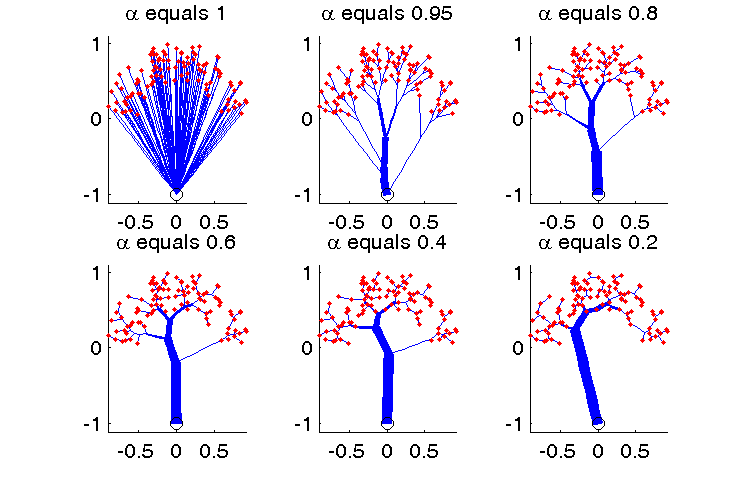
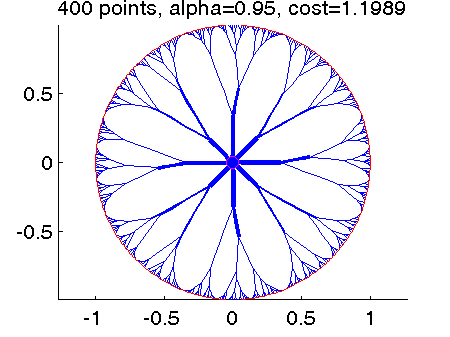
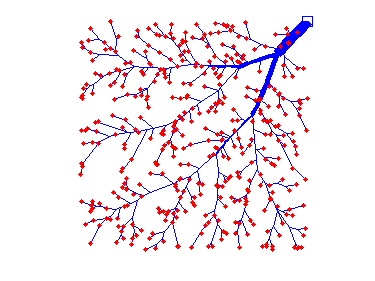
• Example: Given 100 random (red) points and a parameter \alpha in [0,1], an optimal transport path from these points to the origin looks like:

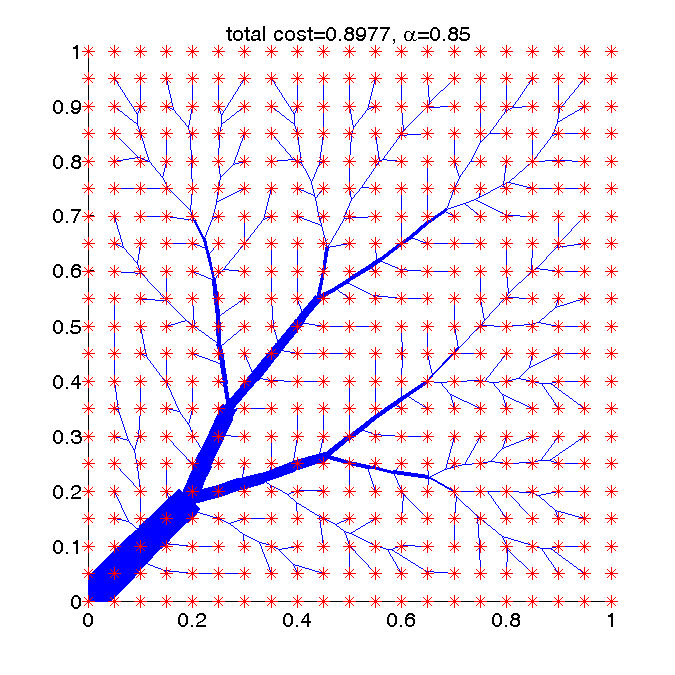
• Example 2: An optimal transport path from uniform distributed points to the origin.

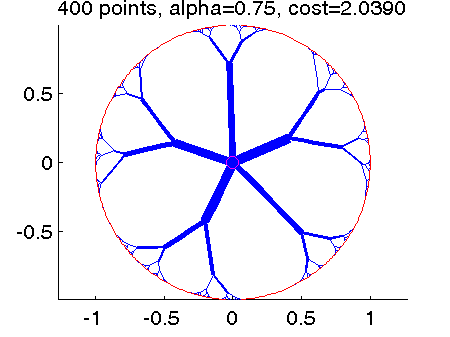
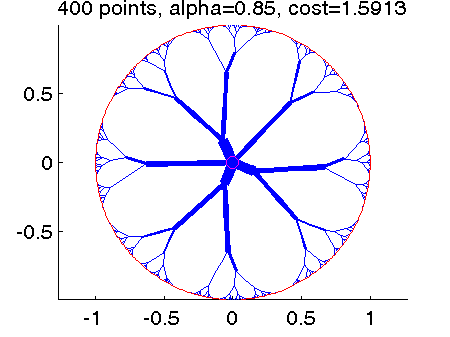
• Example 3: An optimal transport path from a unit circle to its center with different parameter alpha

My future work in this field

• Transport flow
• Optimal fractals

---