UPDATE (December 2024): Jineon Baek has solved the moving sofa problem!
Watch the Numberphile video (watch on YouTube):
The Moving Sofa Problem
Dan Romik
June 2016
—Douglas Adams, "Dirk Gently's Holistic Detective Agency"
The mathematician Leo Moser posed in 1966 the following curious mathematical problem: what is the shape of largest area in the plane that can be moved around a right-angled corner in a two-dimensional hallway of width 1? This question became known as the moving sofa problem, and is still unsolved fifty years after it was first asked.
To understand what makes this question tricky, let's think what kind of "sofa" shapes we can construct that can move around a corner. How about a unit square?
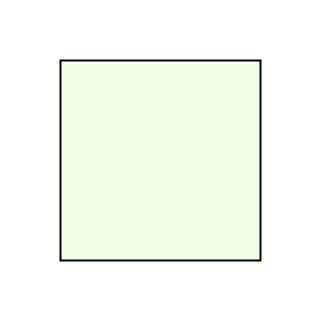
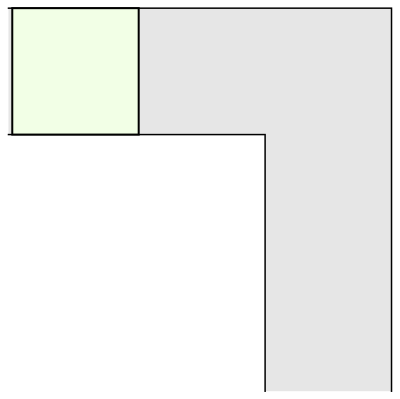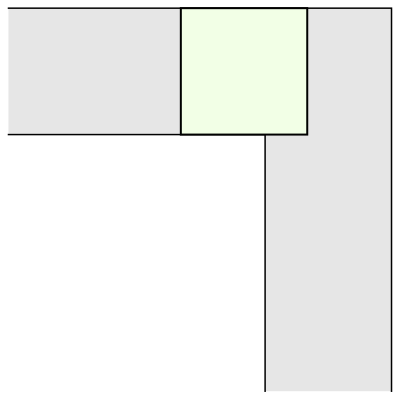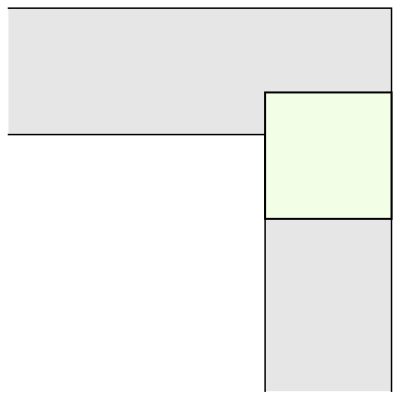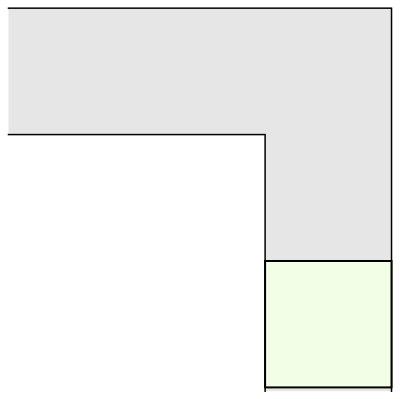
Well, a unit square only has area 1; surely we can do better? For example, a semicircle with radius 1 is another simple example that works:
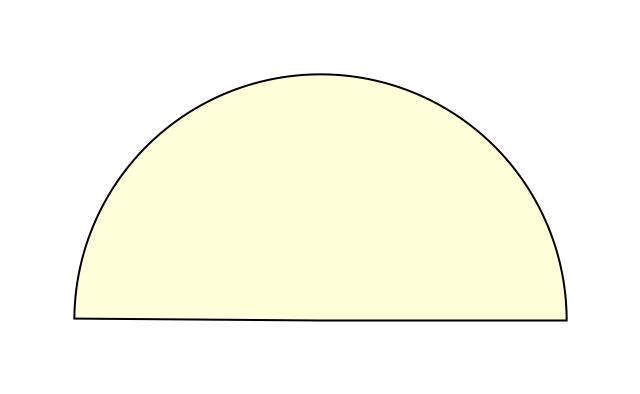
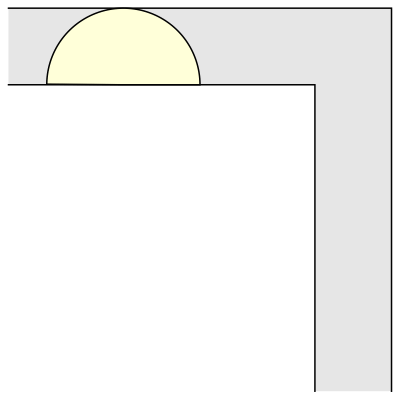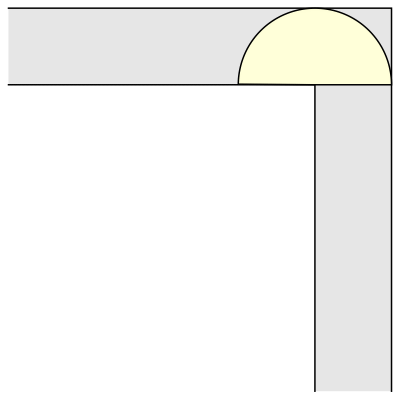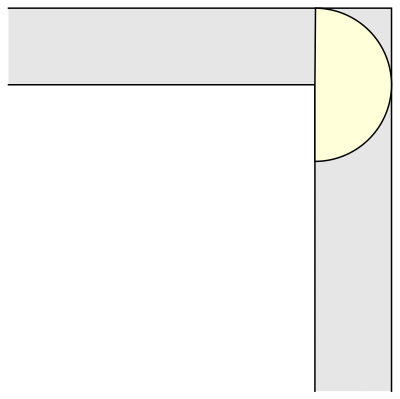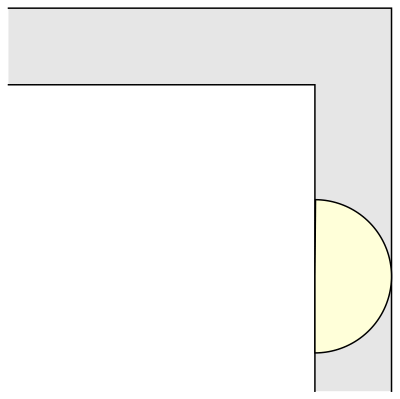
The semicircular sofa has a larger area than the square one, ᴨ/2 (approximately 1.57). It is also more interesting, because in order to move around the corner it rotates, whereas the square sofa merely translates. Now, if only we could combine rotation and translation, maybe we could construct an even bigger sofa shape? Indeed, the mathematician John Hammersley noticed that if the semicircle is cut into two quarter-circles, which are pulled apart and the gap between them filled with a rectangular block, we get a larger sofa shape, which could be moved around the corner if only a smaller semicircular hole is also removed from the rectangular block. Here is the resulting shape, that is starting to look a bit more like an actual sofa:
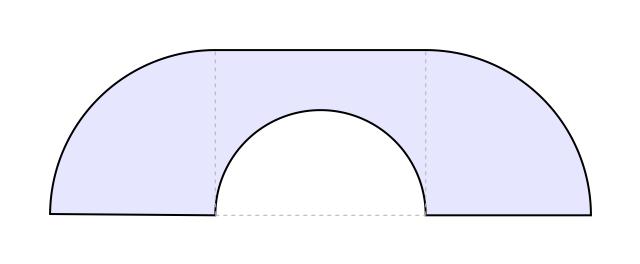
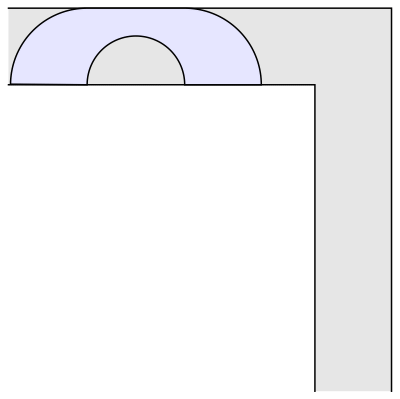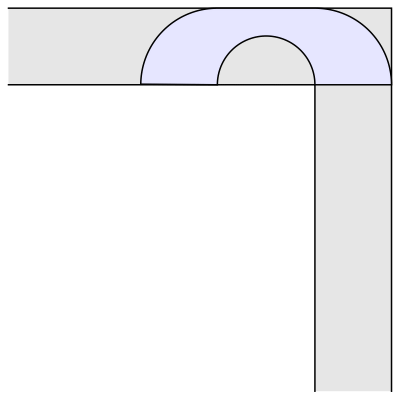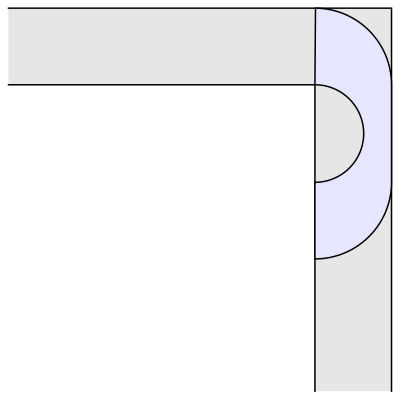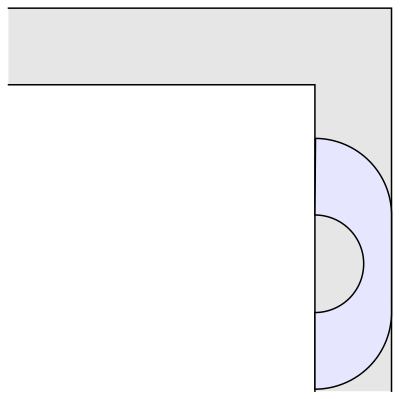
Hammersley's idea works for every value between 0 and 1 of the radius of the semicircular hole at the bottom. The shape of maximal area in this family (shown above) is obtained when the radius is chosen to be 2/ᴨ (approximately 0.637), which gives an area of 2/ᴨ+ᴨ/2, or approximately 2.2074. This is much better than the area of our "idiot's sofa," the unit square. Hammersley thought his construction may be optimal, but this turned out to be false. In 1992, Joseph Gerver found a better shape with a slightly bigger area of around 2.2195. Here it is:
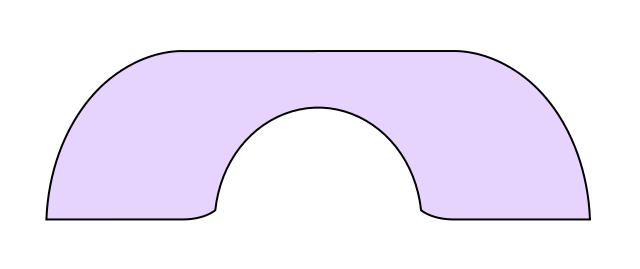
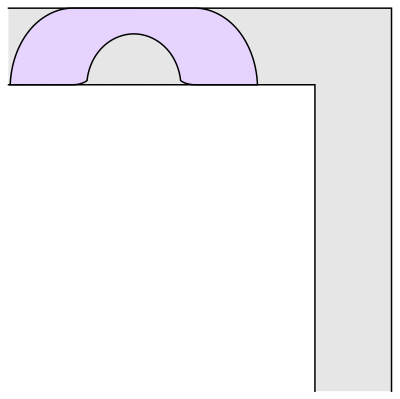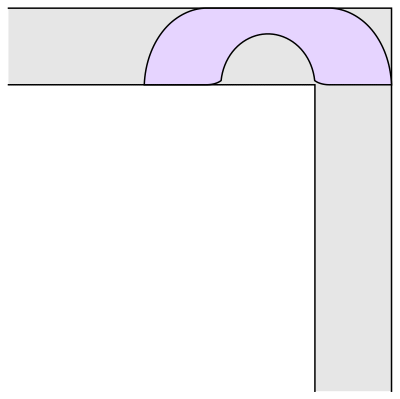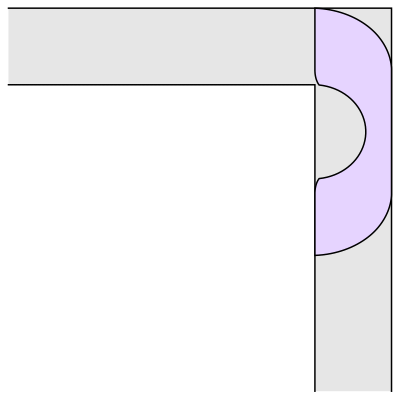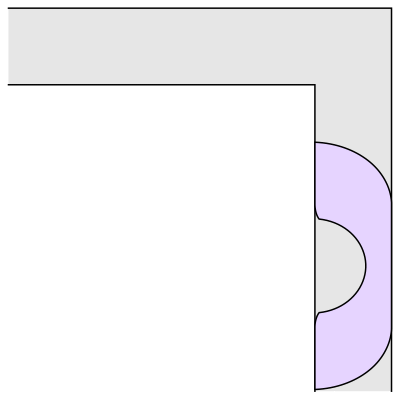
Gerver did not prove that his construction is optimal, but it was derived from considerations of local optimality. Roughly speaking, the area of the shape is in equilibrium when making small perturbations to the path through which the shape is transported to move it around the corner. This leads to differential equations that can be solved to find formulas for the different pieces of the shape (there are 3 straight line segments and 15 curved pieces, each described by its own formula). Thus, it seems quite plausible that Gerver's shape could be the correct solution. Gerver conjectured that it is, and it remains the best one known today.
The moving sofa problem has several other variants. One of them, studied by John Horton Conway and others, asks for the largest area sofa that can be moved around a 90-degree turn both to the right and to the left. By extending the techniques used by Gerver in his 1992 paper, I found such an "ambidextrous sofa" shape with an area of approximately 1.64495, which may be the largest possible area. Here it is:
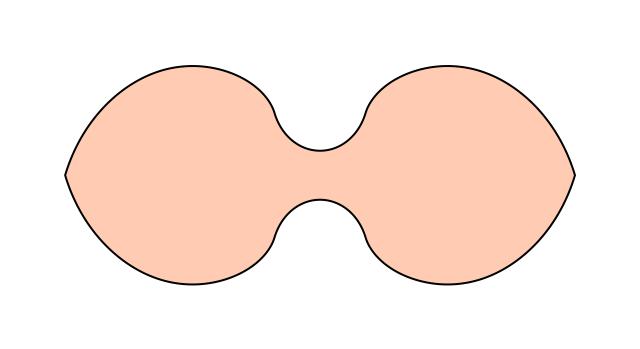
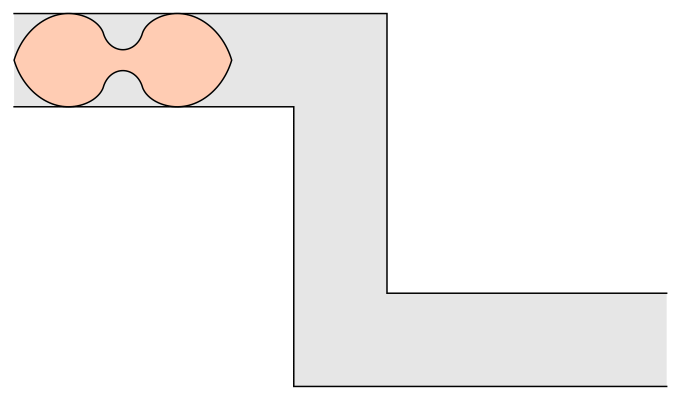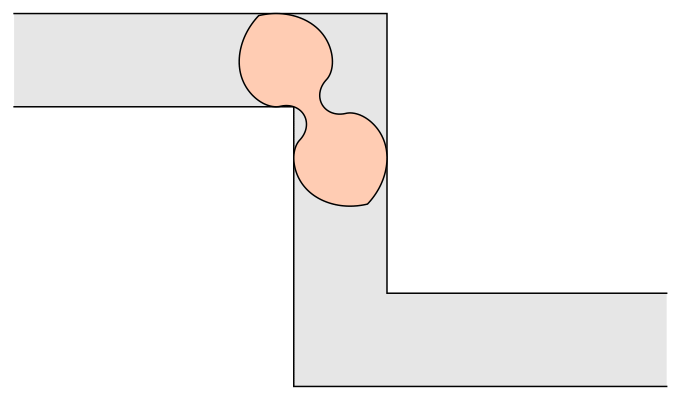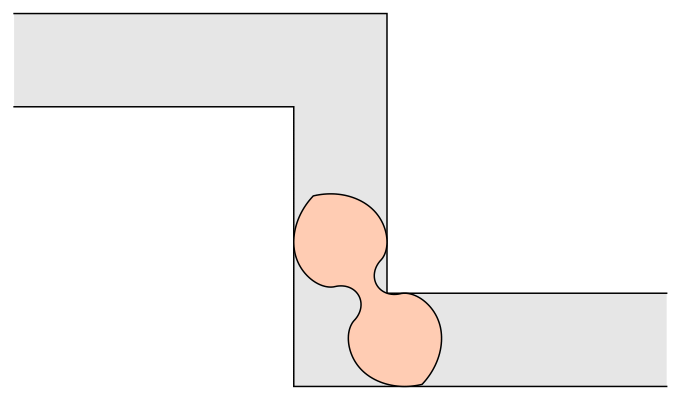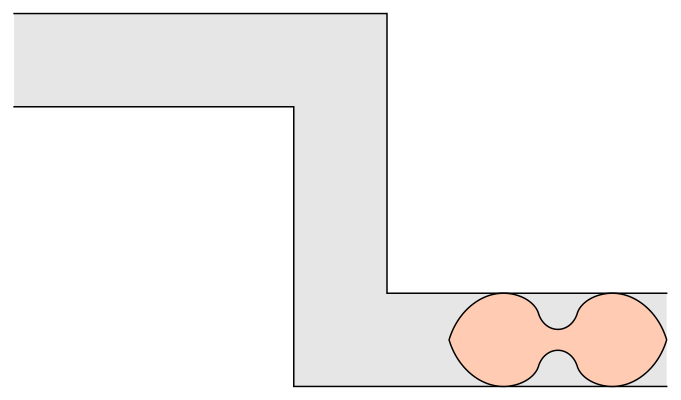
Similar looking shapes were computed numerically using approximation schemes developed by Kiyoshi Maruyama in 1973 and Philip Gibbs in 2014. My derivation yields a solution in closed form for the shape. It has 18 distinct pieces, each of which is given by a separate formula obtained as the solution of some differential equation. The details of the analysis are quite surprising; for example, it turns out that the area of the new shape is given by the unusual formula
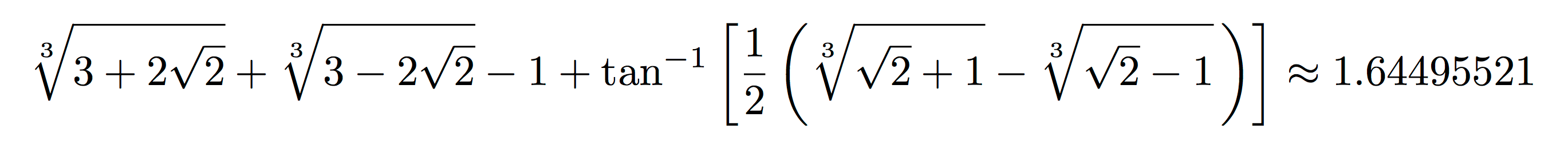
Fifty years after its inception, the moving sofa problem continues to lead to new mathematical insights – and nice-looking pictures and animations! I've also used a 3D printer to create real-life 3D models of the shapes shown above, which are fun to play with and show other people. Check out the downloadable files below that you can use to make similar models for yourself. And if you want to learn more about the mathematics of moving sofas, read my paper and the other references cited below.
The moving sofa problem in the news
- Here is a page with links to recent news articles discussing my work on the moving sofa problem.
References
- D. Romik. Differential equations and exact solutions in the moving sofa problem. Experimental Mathematics 27 (2018), 316-330.
- Y. Kallus, D. Romik. Improved upper bounds in the moving sofa problem. Advances in Mathematics 340 (2018), 960-982.
- Moving sofa problem on Wikiepdia.
- E. W. Weisstein. Moving sofa problem on Wolfram MathWorld.
- J. L. Gerver. On moving a sofa around a corner. Geometriae Dedicata 42 (1992), 267-283. doi:10.1007/BF02414066.
- P. Gibbs. A computational study of sofas and cars. Preprint, 2014.
Downloadable extras
- More animations of moving sofas:
- Hammersley's sofa - sofa-centric view (1.6 MB)
- Gerver's sofa - sofa-centric view (3.8 MB)
- The new ambidextrous sofa - sofa-centric view (3.2 MB)
- Mathematica package: MovingSofas.nb, a companion package to my paper. If you don't have Mathematica, here is a PDF version.
- CAD files for creating 3D models of the shapes shown above (examples: 1, 2):
- L-shaped hallway: hallway.stl (4 KB)
- Hallway with two turns: ambi-hallway.stl (6 KB)
- Semicircular sofa: semicircular.stl (452 KB)
- Hammersley's sofa: hammersley.stl (2.6 MB)
- Gerver's sofa: gerver.stl (2.5 MB)
- The new ambidextrous sofa: ambidextrous.stl (165 KB)