Many of the subjects I've worked on can be illustrated with nice pictures. Below is a collection of mathematical images related to papers I've written. See the references at the bottom for links to the relevant papers and additional information. Additional galleries can be found in these pages:
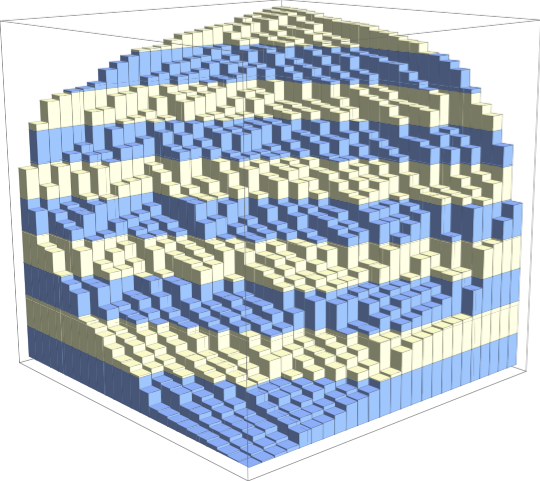
1. A random square Young tableau of order 25, shown on the left as a discrete stepped surface. The smooth surface on the right is the limit shape of such random Young tableaux. The coloring scheme highlights the level curves of both surfaces. [References]
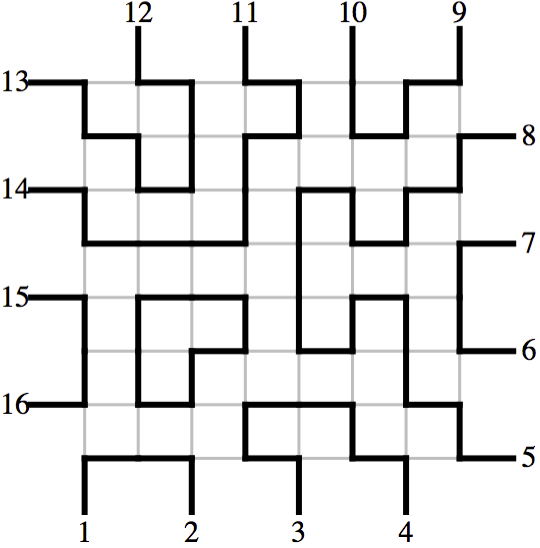
2. The half-way permutation of a random sorting network with 2000 particles. [References and movies]
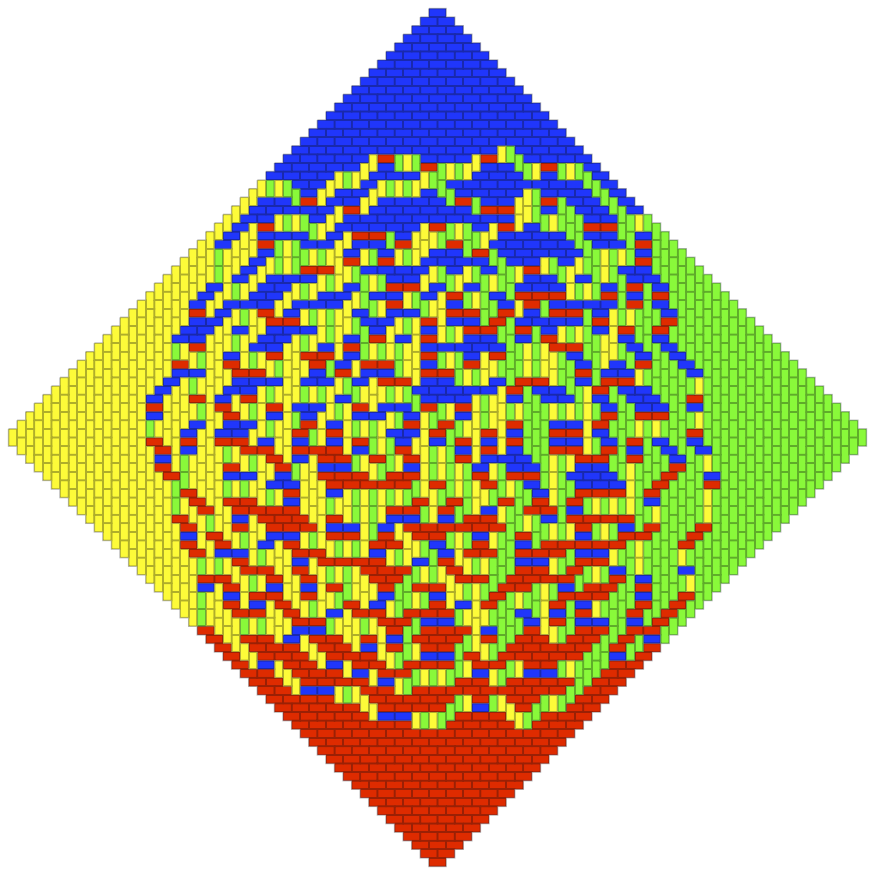
3. A random domino tiling of the Aztec diamond of order 50. [References]
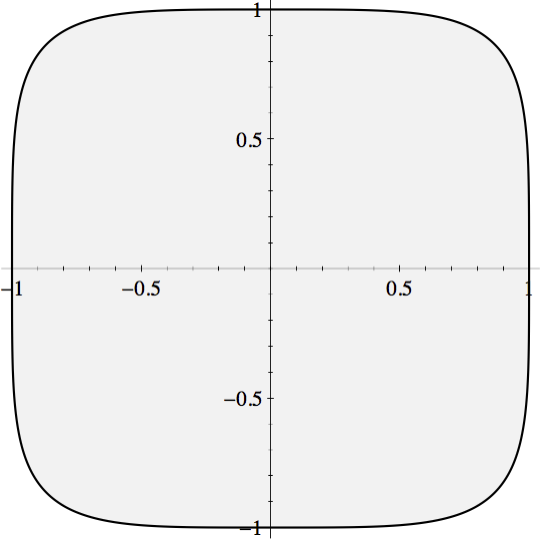
4. A random Erdos-Szekeres permutation of order 50, and the limit shape of such permutations, an algebraic curve of degree 4. [References]
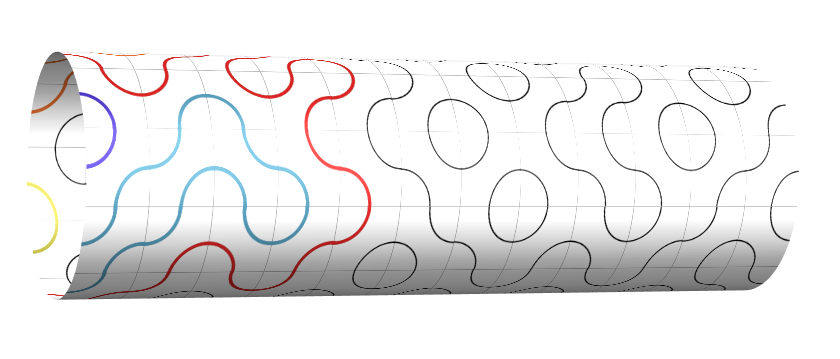
5. Connectivity patterns in loop percolation on a cylinder. [References]
6. A fully packed loop configuration of order 8. [References]
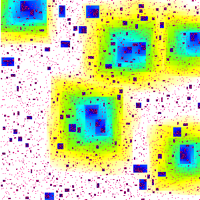
7. Bootstrap percolation (picture by Alexander Holroyd). [References]
8. A tesselation of the hyperbolic plane by quadrilaterals. This is related to a natural dynamical system associated with Pythagorean triples. [References]
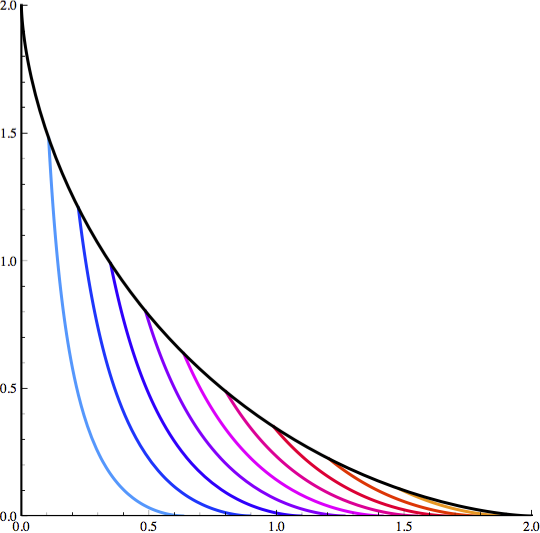
9. Limit shapes of bumping routes in the Robinson-Schensted correspondence. [References]
References
1. Random square Young tableaux
- B. Pittel, D. Romik. Limit shapes for random square Young tableaux. Adv. Appl. Math. 38 (2007), 164-209.
- See also Chapter 3 in my book.
- Random square Young tableaux can be simulated using my Mac simulation app MacTableaux.
2. Random sorting networks
- O. Angel, A. Holroyd, D. Romik, B. Virag. Random sorting networks. Adv. Math. 215 (2007), 839-868.
- D. Dauvergne. The Archimedean limit of random sorting networks. Preprint, 2018.
- Random sorting networks can be simulated using my Mac simulation app MacSort.
- Alexander Holroyd's sorting networks page.
- A movie of a 2000-particle sorting network (.mov file, 3MB)
- Another movie of a random sorting network (time-stationary version; .mov file, 4.3MB)
3. Domino tilings
- D. Romik. Arctic circles, domino tilings and square Young tableaux. Ann. Probab. 40 (2012), 611-647.
- The arctic circle theorem (Wikipedia).
- See also my Mac simulation apps MacTableaux and ASM Simulator.
4. Erdos-Szekeres permutations
- D. Romik. Permutations with short monotone subsequences. Adv. Appl. Math. 37 (2006), 501-510.
- See also Chapter 3 in my book.
5-6. Connectivity patterns in loop percolation, fully packed loops
- D. Romik. Connectivity patterns in loop percolation I: the rationality phenomenon and constant term identities. Commun. Math. Phys. 330 (2014), 499-538.
- Fully packed loops are also studied under the name alternating sign matrices, which I studied in the papers:
- I. Fischer, D. Romik. More refined enumerations of alternating sign matrices. Adv. Math. 222 (2009), 2004-2035.
- M. Karklinsky, D. Romik. A formula for a doubly refined enumeration of alternating sign matrices. Adv. Appl. Math. 45 (2010), 28-35.
- A. Ayyer, D. Romik. New enumeration formulas for alternating sign matrices and square ice partition functions. Adv. Math. 235 (2013), 161-186.
7. Bootstrap percolation
- A. Holroyd, T. Liggett, D. Romik. Integrals, partitions and cellular automata. Trans. Amer. Math. Soc. 356 (2004), 3349-3368.
- Alexander Holroyd's bootstrap percolation page.
8. Tesselation of the hyperbolic plane by quadrilaterals
- D. Romik. The dynamics of Pythagorean triples. Trans. Amer. Math. Soc. 360 (2008), 6045-6064.
9. Bumping routes in the Robinson-Schensted correspondence
- D. Romik, P. Sniady. Limit shapes of bumping routes in the Robinson-Schensted correspondence. Random Struct. Algor. 48 (2016), 171-182.
- This paper and the above picture answer a question posed by Cris Moore in 2006 on his gallery page (scroll to the section titled "Flows in Young diagrams").
- The bumping routes can also be experimented with using my Mac simulation app MacTableaux.