My software projects can be found below, or on my GitHub page.
Typesetting software
- MadHat - MacOS software for writing documents and presentations
Educational software
- Calculus widgets - interactive demos of calculus concepts developed for a class I was teaching
Research software
My coauthors and I have written several software packages as an aid to studying various interesting mathematical objects.
- A Mathematica package OrientedSwaps. This is a companion package to the paper "Staircase Young tableaux, sorting networks and last passage percolation" written jointly with Elia Bisi, Fabio Cunden and Shane Gibbons.
- SofaBounds: A software package for computer-assisted proofs in the moving sofa problem. A Unix command line tool, written in C++, that is a companion package to the paper "Improved upper bounds in the moving sofa problem" written jointly with Yoav Kallus.
- A Mathematica package MovingSofas, or a PDF version. This is a companion package to the paper "Differential equations and exact solutions in the moving sofa problem."
- A Mathematica notebook SU3-ASYM.nb, or a PDF version. This is a companion package to the paper "On the number of n-dimensional representations of SU(3), the Witten zeta function, and the Bernoulli numbers."
- A Mathematica-based slide presentation titled "The combinatorics of fully packed loops and Razumov-Stroganov conjectures", which I presented on Aug. 8, 2014 at MAA MathFest 2014. Download the Mathematica notebook of the presentation, written in Mathematica 8, or a (non-interactive) PDF version. The notebook contains as embedded code two Mathematica function libraries I wrote, linkpatterns.m and loops.m, that implement many operations and several interactive simulations related to fully packed loops, noncrossing matchings and related mathematical objects.
- A Maple package RefinedASM1234.txt. This is a companion package to my paper "New enumeration formulas for alternating sign matrices and square ice partition functions" written jointly with Arvind Ayyer.
- A Mathematica notebook GammaDelta.nb. Another companion package to the same paper with Arvind Ayyer. This notebook verifies a claim added in the revised version of the paper.
- A Mathematica notebook RefinedASM.nb. This is a companion package to the paper "More refined enumerations of alternating sign matrices" written jointly with Ilse Fischer.
Software written by students who worked on research projects with me
- A SageMath package qKZ, written by Joshua Sumpter. This package implements operations on wheel polynomials, a family of polynomials described in my paper "Connectivity patterns in loop percolation I: the rationality phenomenon and constant term identities".
- Sofa_gui.py: a Python application written by Jordan Fields for numerically optimizing shapes in the moving sofa problem.
Mac simulation software
Here is some software I’ve written to simulate some interesting mathematical objects I’m thinking about. It runs on any Mac running Mac OS version 10.5 and higher.
Update (November 2020): I have posted new versions of the MacTableaux and MacSort app binaries that have been recompiled to run on the Intel 64-bit architecture. So you can now run these apps on Macs running MacOS 10.15 and higher. The old 32-bit binary versions are also included in the download package.
Click icon to download
(356 KB zip file)
(356 KB zip file)
ASM Simulator
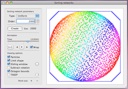
A program for experimenting with random alternating sign matrices and domino tilings of the Aztec diamond. It lets you visualize alternating sign matrices in several ways and witness the remarkable Arctic Circle Theorem for random domino tilings. The mathematics behind this is described in several papers. You can find a bibliography and some more information in the application itself by clicking the button marked “?”. The download package includes the source code, written in Objective-C.
A program for experimenting with random alternating sign matrices and domino tilings of the Aztec diamond. It lets you visualize alternating sign matrices in several ways and witness the remarkable Arctic Circle Theorem for random domino tilings. The mathematics behind this is described in several papers. You can find a bibliography and some more information in the application itself by clicking the button marked “?”. The download package includes the source code, written in Objective-C.
Click icon to download
(44 KB zip file)
(44 KB zip file)
Allocation
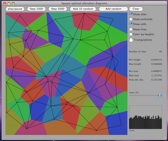
A program for experimenting with optimal and fair allocation of areas to points in a square domain. Starting from the Voronoi diagram, the areas of the cells allocated to the points are adjusted until all areas are equal. The theoretical idea behind this construction is described in the paper Minkowski-type theorems and least-squares clustering, by F. Aurenhammer, F. Hoffmann and B. Aronov, [Algorithmica 20 (1998), 61-76], and in the context of analyzing the behavior for random points was suggested to me by Yuliy Baryshnikov.
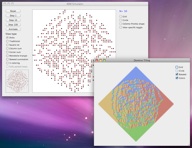
A program for experimenting with optimal and fair allocation of areas to points in a square domain. Starting from the Voronoi diagram, the areas of the cells allocated to the points are adjusted until all areas are equal. The theoretical idea behind this construction is described in the paper Minkowski-type theorems and least-squares clustering, by F. Aurenhammer, F. Hoffmann and B. Aronov, [Algorithmica 20 (1998), 61-76], and in the context of analyzing the behavior for random points was suggested to me by Yuliy Baryshnikov.
Click icon to download
(459 KB zip file)
(459 KB zip file)
MacTableaux
A program for experimenting with random Young diagrams and random Standard Young Tableaux (SYT’s). Simulate Plancherel measure on the set of Young diagrams, Rost’s corner growth model for random Young diagrams, or uniformly random SYT of given shape (including the cases of square, rectangular, and staircase shapes which my coauthors and I have studied). Also implemented are the Robinson-Schensted algorithm, the jeu de taquin sliding operations, and the non-crossing path interpretation of SYT’s.
A program for experimenting with random Young diagrams and random Standard Young Tableaux (SYT’s). Simulate Plancherel measure on the set of Young diagrams, Rost’s corner growth model for random Young diagrams, or uniformly random SYT of given shape (including the cases of square, rectangular, and staircase shapes which my coauthors and I have studied). Also implemented are the Robinson-Schensted algorithm, the jeu de taquin sliding operations, and the non-crossing path interpretation of SYT’s.
Click icon to download
(717 KB zip file)
(717 KB zip file)
MacSort
A program for experimenting with random sorting networks, a.k.a. reduced word representations of the maximal permutation. The two main random models are the Uniform Sorting Networks (USN), which were studied in the paper Random Sorting Networks, by O. Angel, A. E. Holroyd, B. Virag and myself [Adv. Appl. Math. 215 (2007), 839-868], and the Oriented Swap Process, discussed in the paper The Oriented Swap Process, by O. Angel, A. E. Holroyd and myself [Ann. Probab. 37 (2009), 1970-1998].
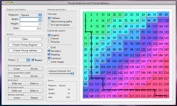
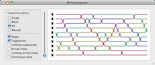
A program for experimenting with random sorting networks, a.k.a. reduced word representations of the maximal permutation. The two main random models are the Uniform Sorting Networks (USN), which were studied in the paper Random Sorting Networks, by O. Angel, A. E. Holroyd, B. Virag and myself [Adv. Appl. Math. 215 (2007), 839-868], and the Oriented Swap Process, discussed in the paper The Oriented Swap Process, by O. Angel, A. E. Holroyd and myself [Ann. Probab. 37 (2009), 1970-1998].
