This page will always be under construction!


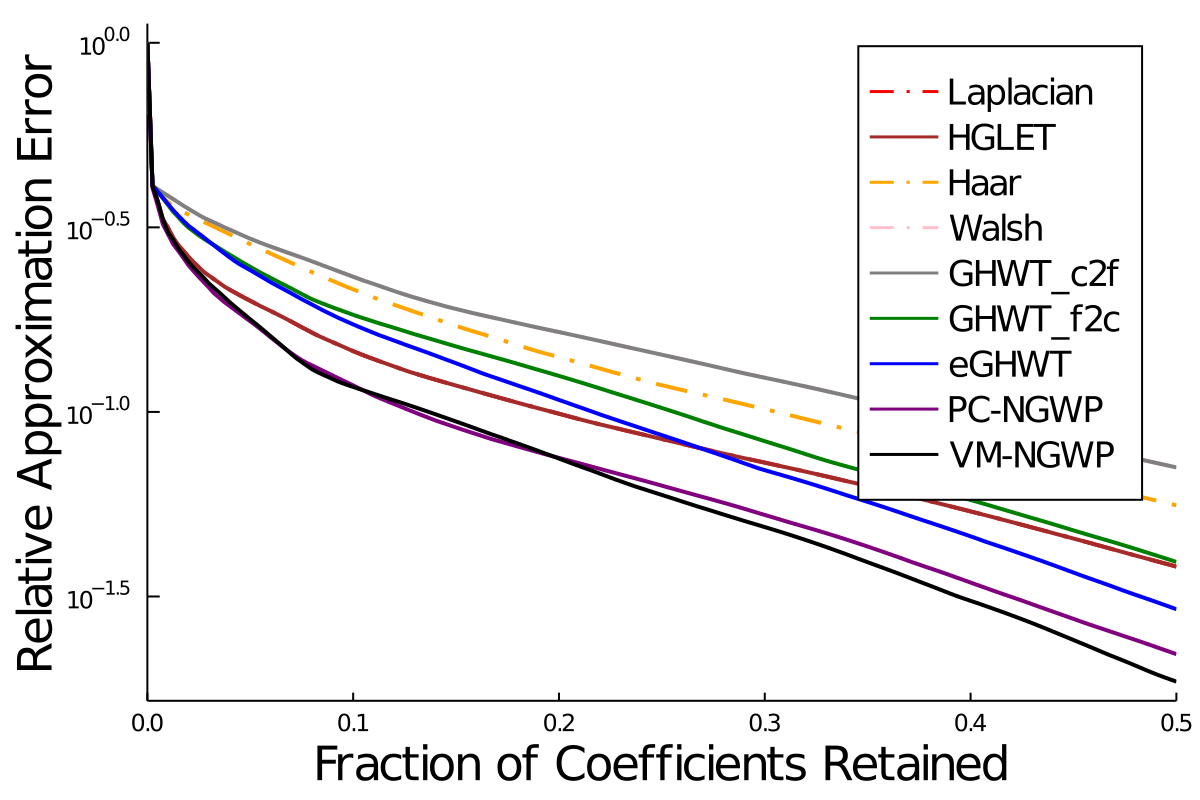
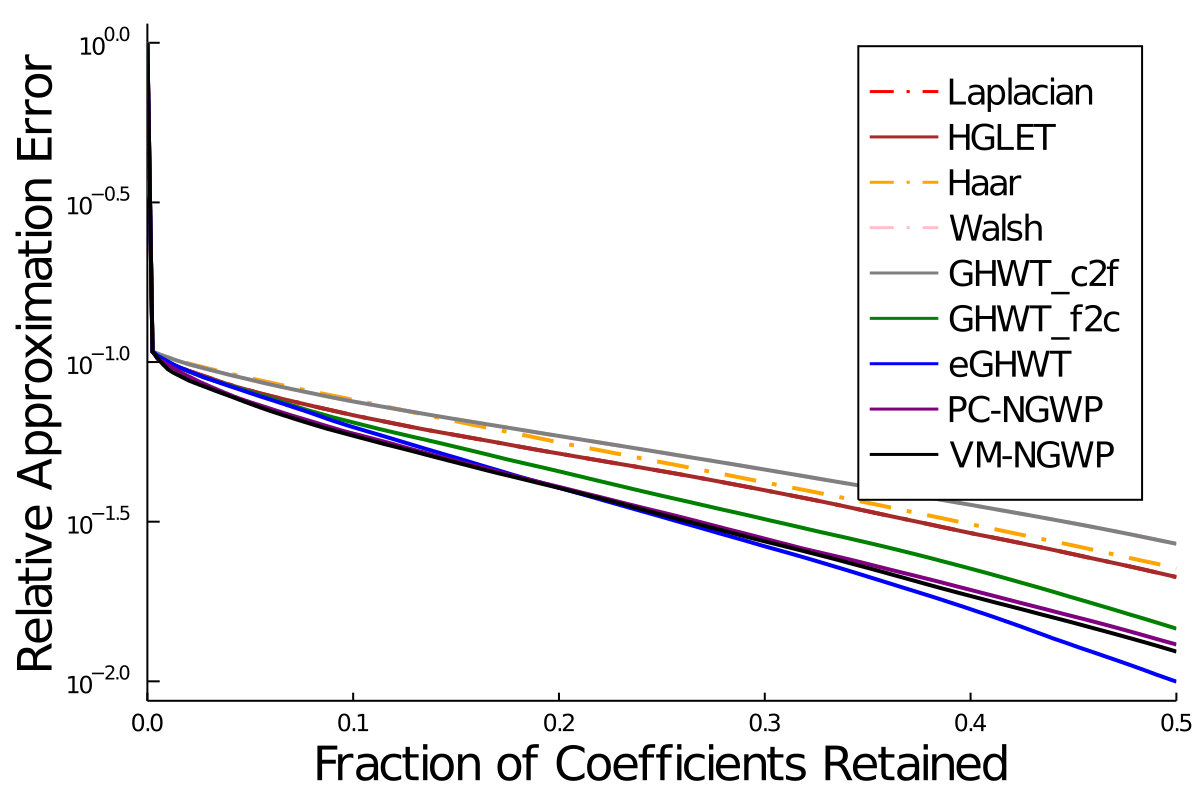
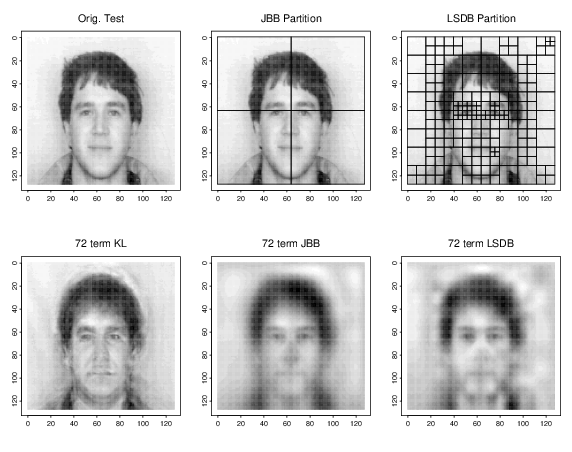
| Method | Training (%) | Test (%) |
|---|---|---|
| LDA on raw inputs | 0.83 | 12.31 |
| CT on raw inputs | 2.83 | 11.28 |
| LDA on top 10 LDB coordinates | 7.00 | 8.37 |
| CT on top 10 LDB coordinates | 2.67 | 5.54 |
| CT on all LDB coordinates | 2.33 | 7.60 |




A long time ago, when I was a college student, I was told: "There is good mathematics around Laplacians." I engaged in mathematical research and education for a long time, but after all, I was just walking around "Laplacians," which appear in all sorts of places under different guises. When I reflect on the above adage, however, I feel keenly that it represents an aspect of the important truth. I was ignorant at that time, but it turned out that "Laplacians" are one of the keywords to understand the vast field of modern mathematics.I strongly agree with that adage, and also want to add: "There are really good applications in science and engineering around Laplacians too."
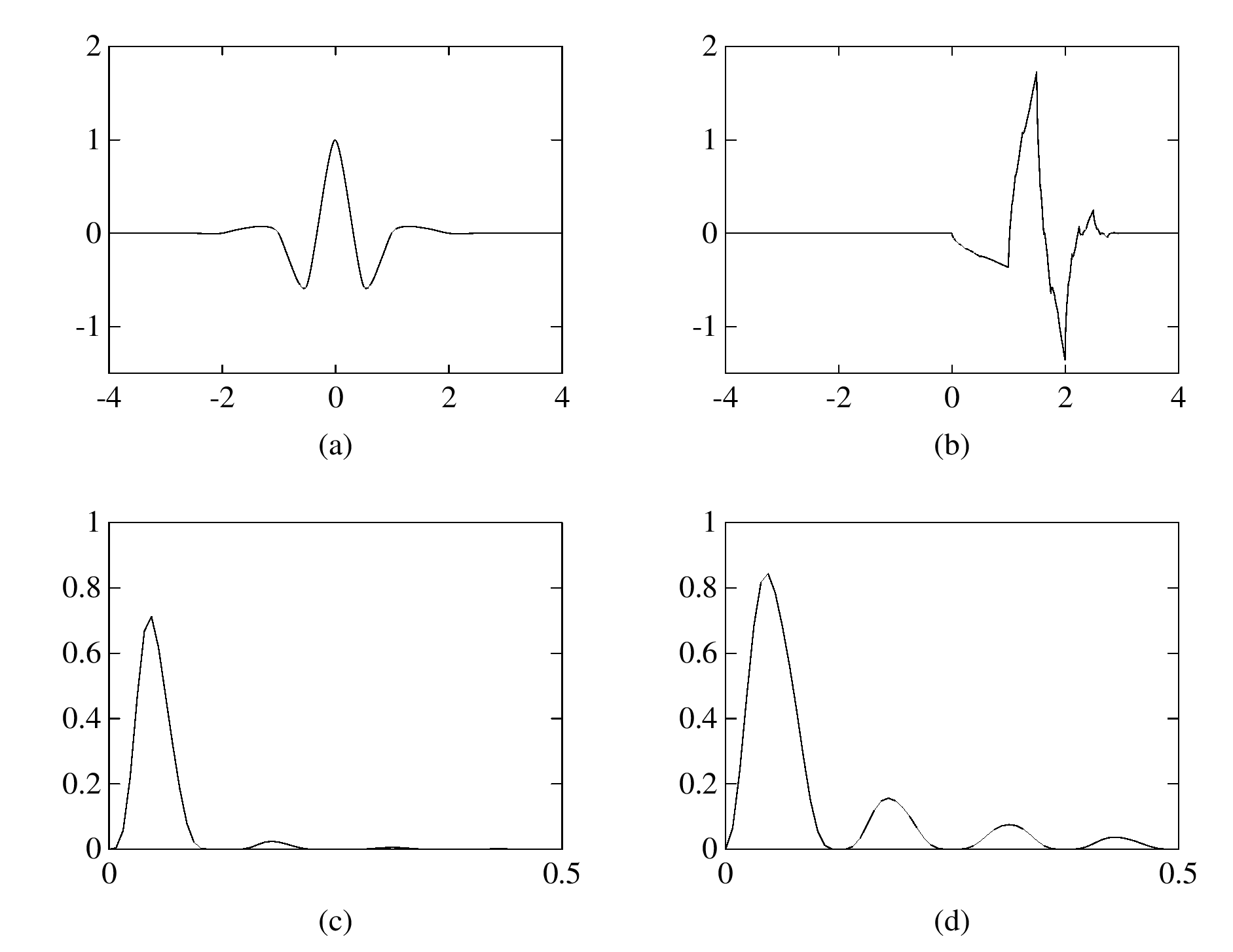
The integral operator \(\mathcal{K}\) commutes with the Laplacian \(\mathcal{L}) with the above nonlocal boundary condition. Consequently, the integral operator \(\mathcal{K}\) is compact and self-adjoint on \(L^2(\Omega)\). Thus, the kernel \(K(\boldsymbol{x},\boldsymbol{y})\) has the following eigenfunction expansion (in the sense of mean convergence): $$ K(\boldsymbol{x},\boldsymbol{y}) \sim \sum_{j=1}^\infty \mu_j \varphi_j(\boldsymbol{x})\overline{\varphi_j(\boldsymbol{y})}, $$ and \(\{ \varphi_j \}_{j \in \mathbb{N}}\) forms an orthonormal basis of \(L^2(\Omega)\).It turned out that such eigenfunctions \(\{\varphi_j\}\) satisfy the following peculiar extension to the outside of \(\Omega\):
The eigenfunction \(\varphi(\boldsymbol{x})\) of the integral operator \(\mathcal{K}\) in the previous theorem can be \(\color{orange}{\textit{extended}}\) outside the domain \(\Omega\) and satisfies the following equation: $$ -\varDelta \varphi = \begin{cases} \lambda \, \varphi & \text{if \(\boldsymbol{x} \in \Omega\)}; \\ 0 & \text{if \(\boldsymbol{x} \in \mathbb{R}^d\setminus\overline{\Omega}\)} , \end{cases} $$ with the boundary condition that \(\varphi\) and \(\partial_\nu \varphi\) are continuous \(\color{orange}{\textit{across}}\) the boundary \(\partial \Omega\). Moreover, as \(|\boldsymbol{x}| \to \infty\), \(\varphi(\boldsymbol{x})\) must be of the following form: $$ \varphi(\boldsymbol{x}) = \begin{cases} \mathrm{const} \cdot | \boldsymbol{x} |^{2-d} + O(|\boldsymbol{x}|^{1-d}) & \text{if \(d \neq 2\)}; \\ \mathrm{const} \cdot \ln | \boldsymbol{x} | + O(|\boldsymbol{x}|^{-1}) & \text{if \(d = 2\)}. \end{cases} $$It would be really nice if one could give physical interpretation to this problem: what is the physical phenomenon that is oscillatory inside \(\Omega\) and is harmonic outside \(\Omega\)?



Let \(\{ \lambda_n \}_{n=0}^\infty\) be the eigenvalues of the nonlocal boundary value problem associated with the harmonic kernel \(K(x,y)=-|x-y|/2\) on \(\Omega=(0,1)\). Let \(K_p(x,y)\) be the \(p\)th iterated kernel of \(K(x,y)\). Then, we have $$ \sum_{n=0}^\infty \frac{1}{\lambda^p_n} = \int_0^1 K_p(x,x) \, \mathrm{d}x = \frac{1}{4^p} \left( S_{2p} + \frac{(-1)^p}{\alpha^{2p}} \right) + \frac{4^p-1}{2 \cdot (2p)!} |B_{2p}|, $$ where \(\displaystyle S_{2p} = \sum_{m=1}^\infty \left( \frac{4}{\lambda_{2m}} \right)^p \), \(\alpha \approx 1.19967864\) is a unique root of \(\alpha = \coth \alpha\), and \(B_{2p}\) is the Bernoulli number, which is defined via the generating function: \(\displaystyle \frac{x}{\mathrm{e}^x-1} = \sum_{n=0}^\infty \frac{B_n}{n!}x^n \). Moreover, \(S_{2p}\) satisfies the following recursion formula: $$ \sum_{\ell=1}^{n+1} \frac{(-1)^{n-\ell+1} \left( 2\left(n-\ell+1\right)-1\right)}{\left( 2\left(n-\ell+1\right)\right)!} \left\{ S_{2\ell} + \frac{(-1)^\ell}{\alpha^{2\ell}} \right\} = \frac{(-1)^n}{2(2n)!}. $$Note that setting \(p=1\) in the above formula, we have \(\displaystyle \sum_{n=0}^\infty \frac{1}{\lambda_n} = 0\). Our results were published in July 2018 in the journal Applied and Computational Harmonic Analysis.
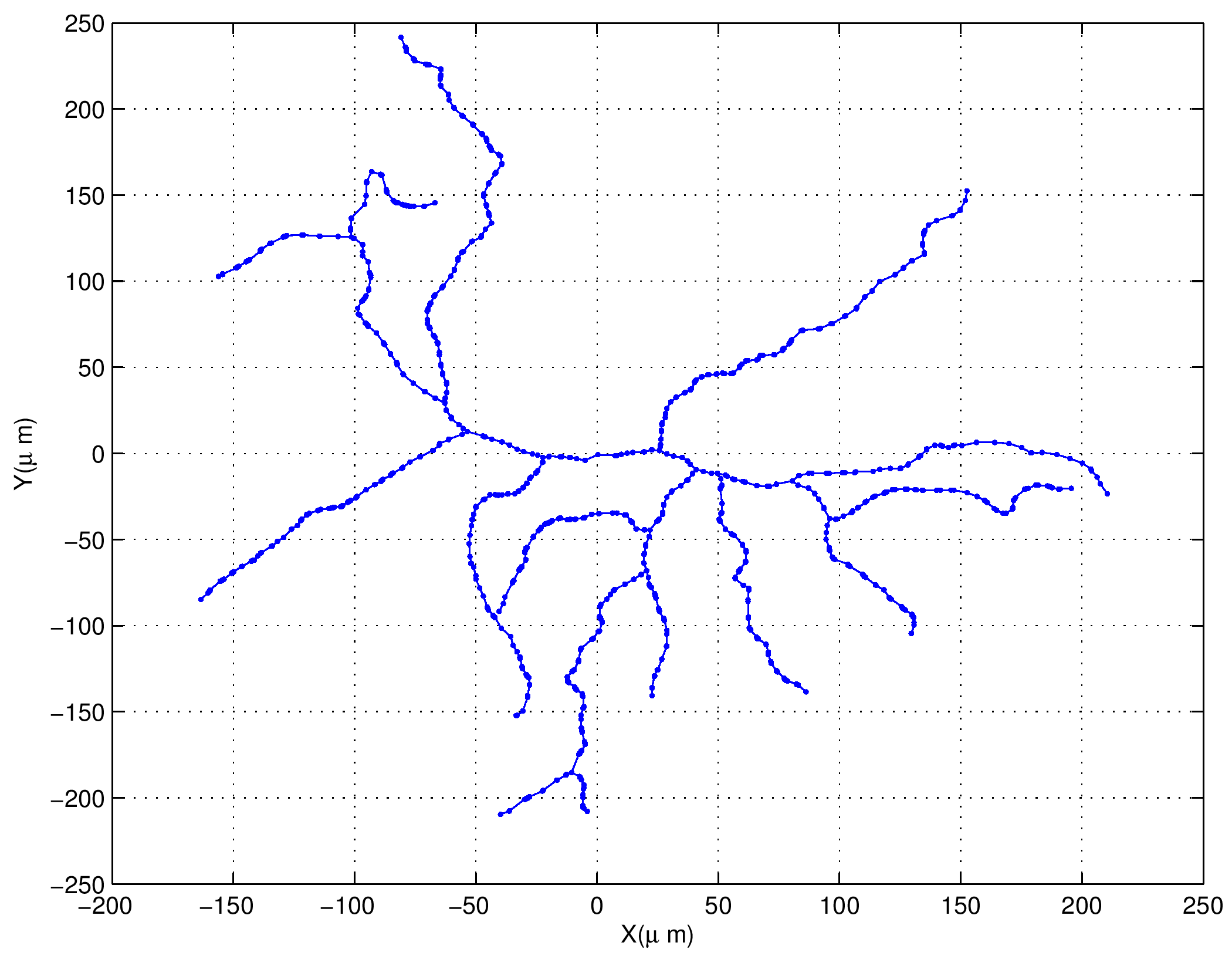
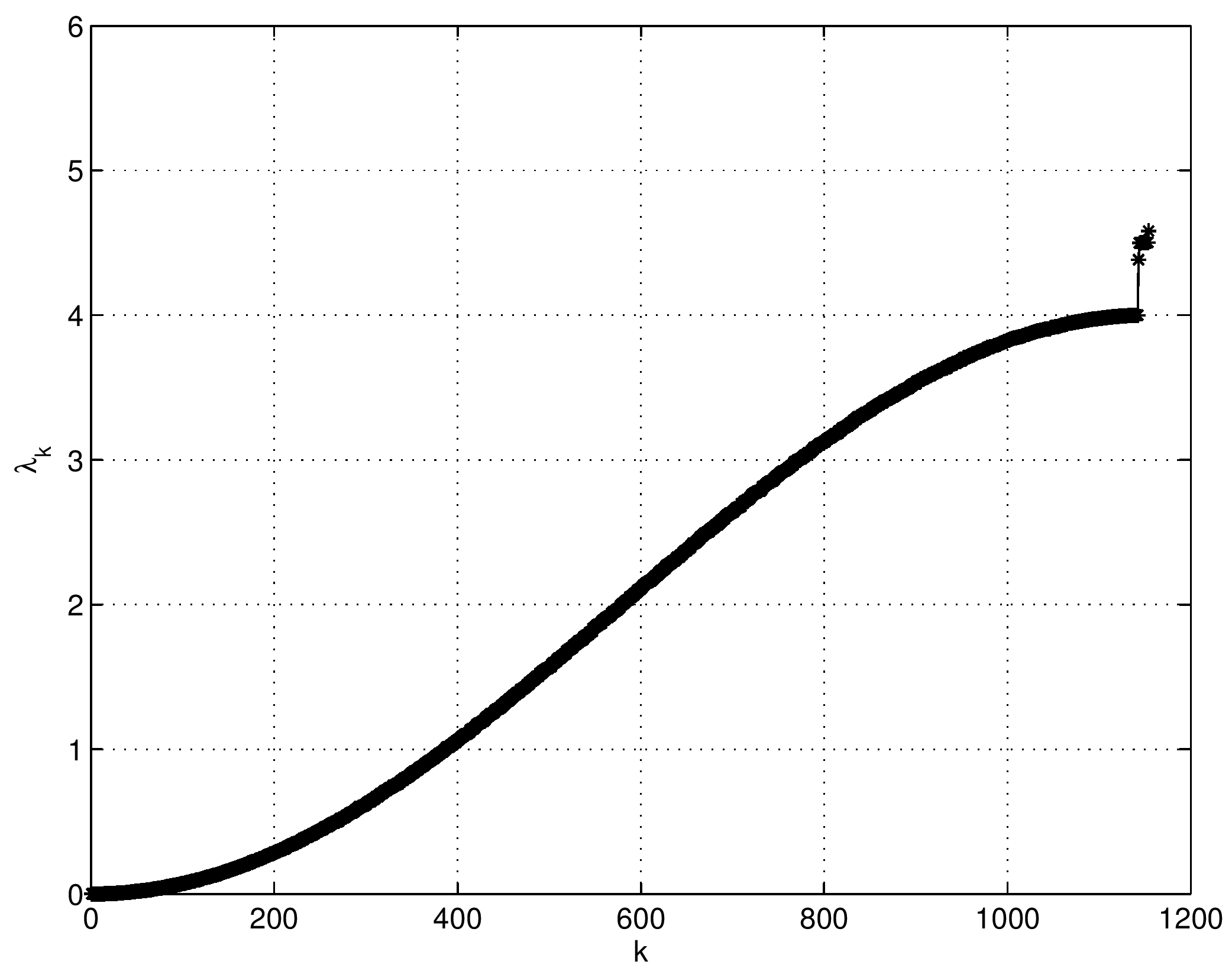
Let \(G(V,E)\) be a simple, connected, undirected, and unweighted graph with \(n=|V|\). Let \(\theta = \frac{3-\sqrt{5}}{2}\) and \(\theta^* = \frac{3+\sqrt{5}}{2}\). Let \(\tau\) be the difference between: 1) the number of degree 2 nodes each of which is adjacent to a leaf node and a node whose degree is 3 or higher; and 2) the number of the latter high degree nodes. Suppose \(\tau \geq 1\), then $$ m_G(\theta) = m_G(\theta^*) \geq \tau . $$ In other words, the multiplicity of the graph Laplacian eigenvalues \(\theta\) and that of \(\theta^*\) are the same and at least \(\tau\).Our results were published in Linear Algebra & its Applications in September 2015. This paper certainly drew attention from a group of mathematicians. In our paper, we also stated our conjecture: the difference between the number of the specially-qualified pendant vertices and their neighbors is bounded from above by the multiplicity of a certain graph Laplacian eigenvalue. This conjecture was proved in August 2016, and the generalized version of our conjecture for signless Laplacians has been also proved in October 2016.
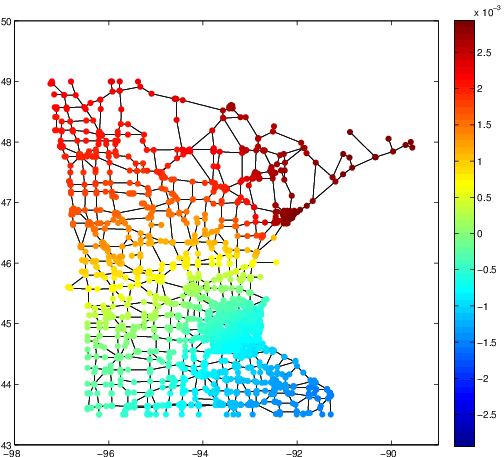
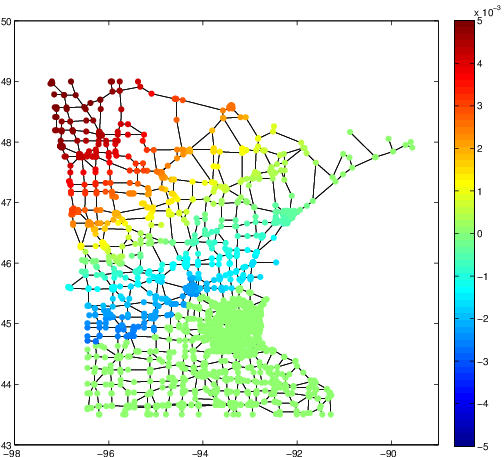
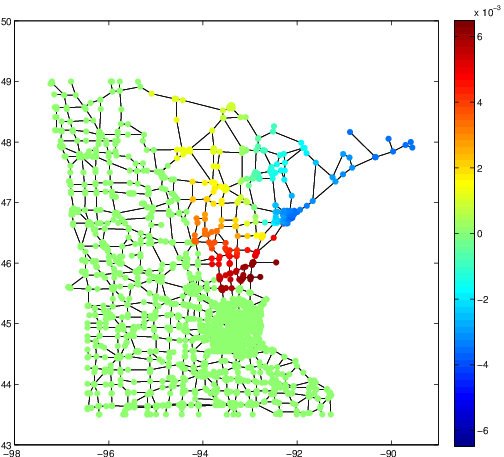
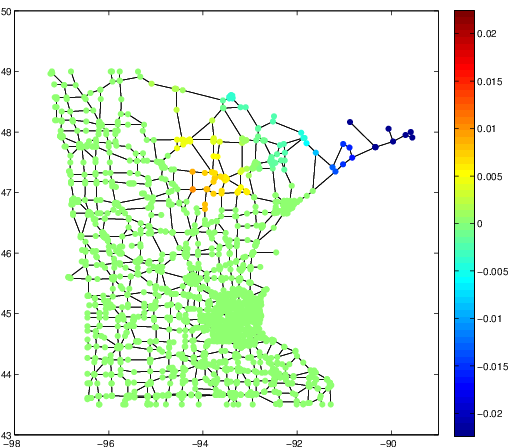
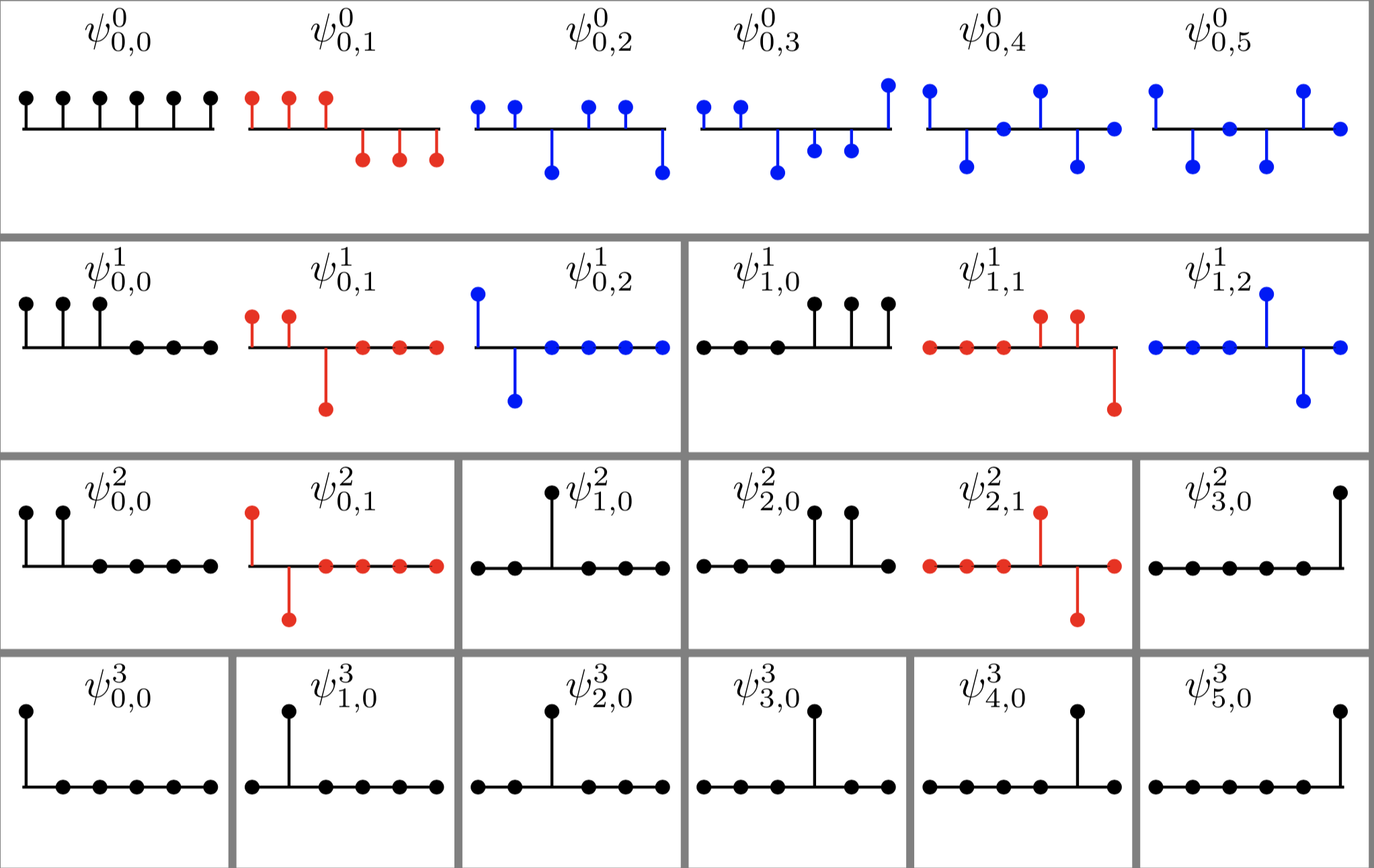
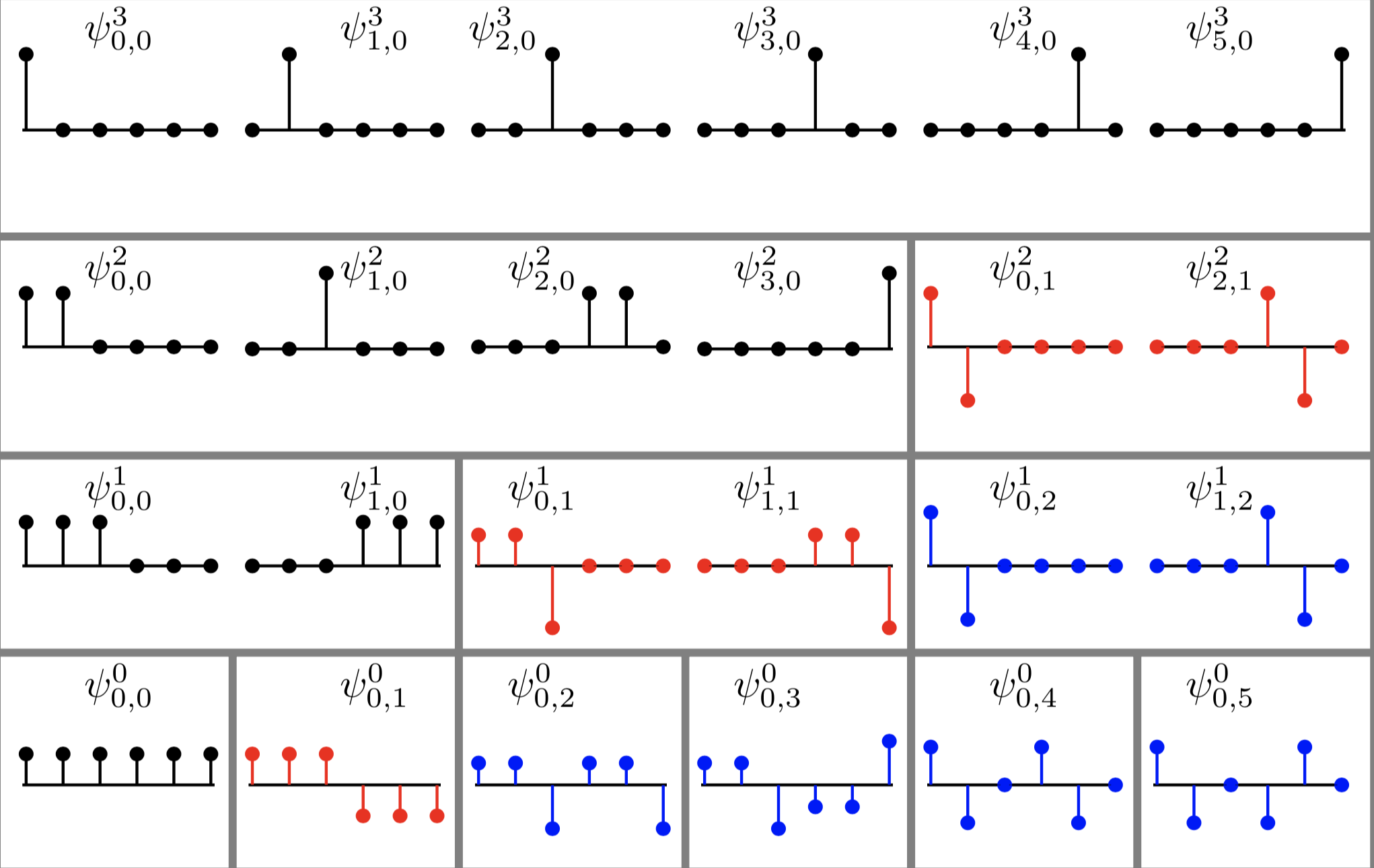
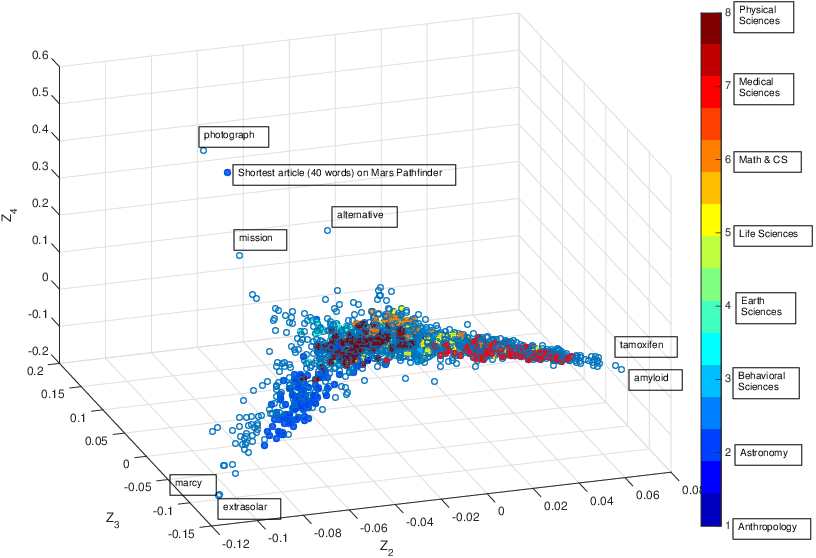

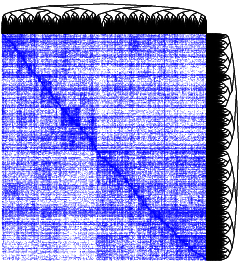
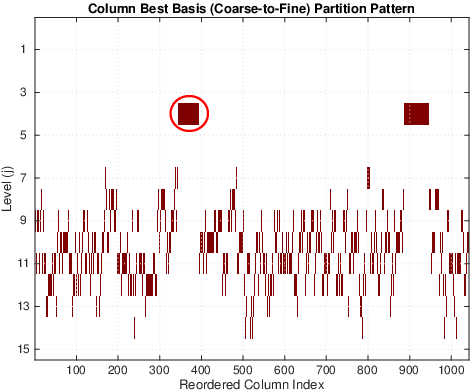
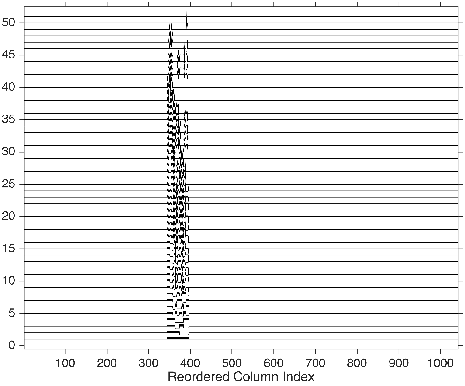
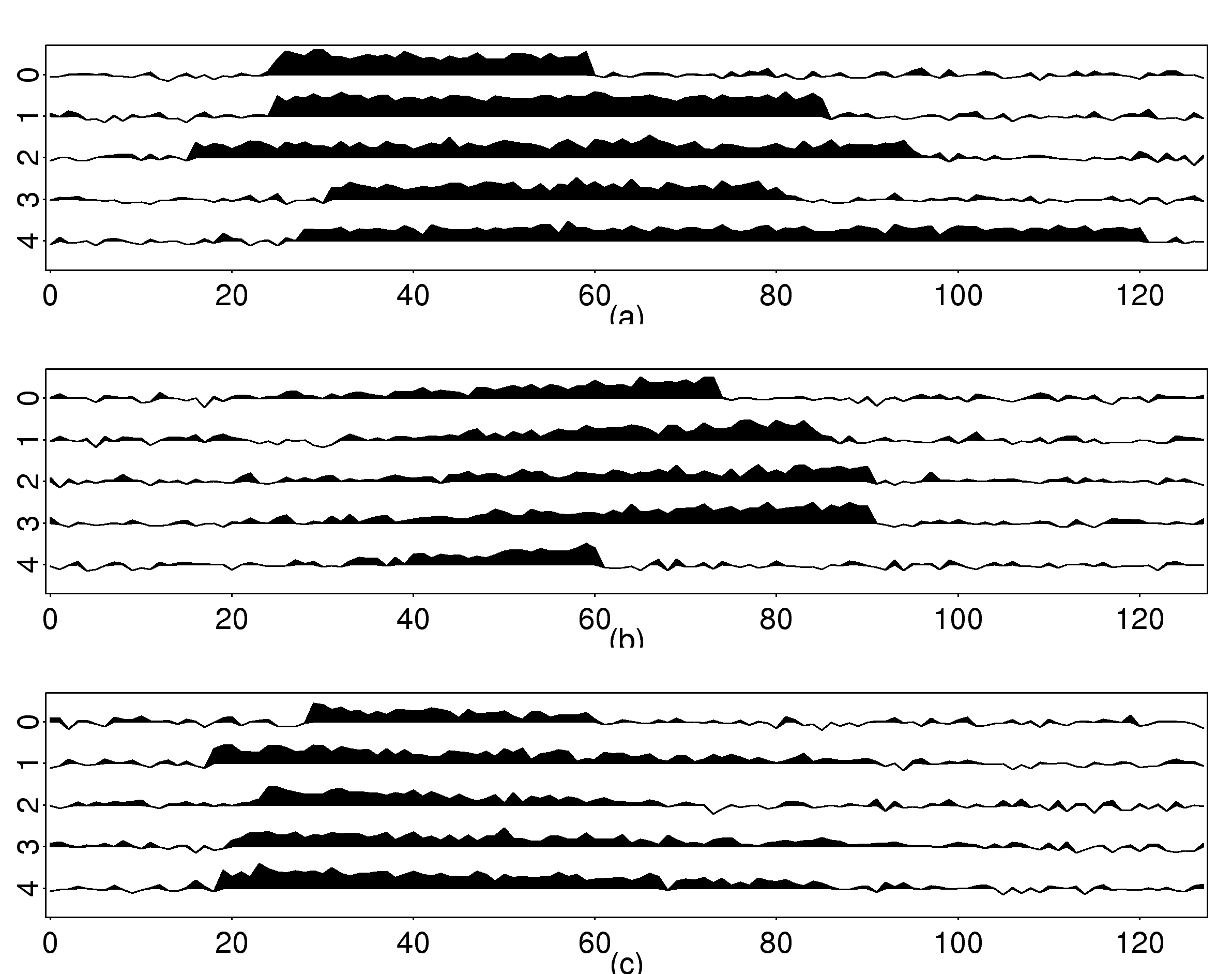
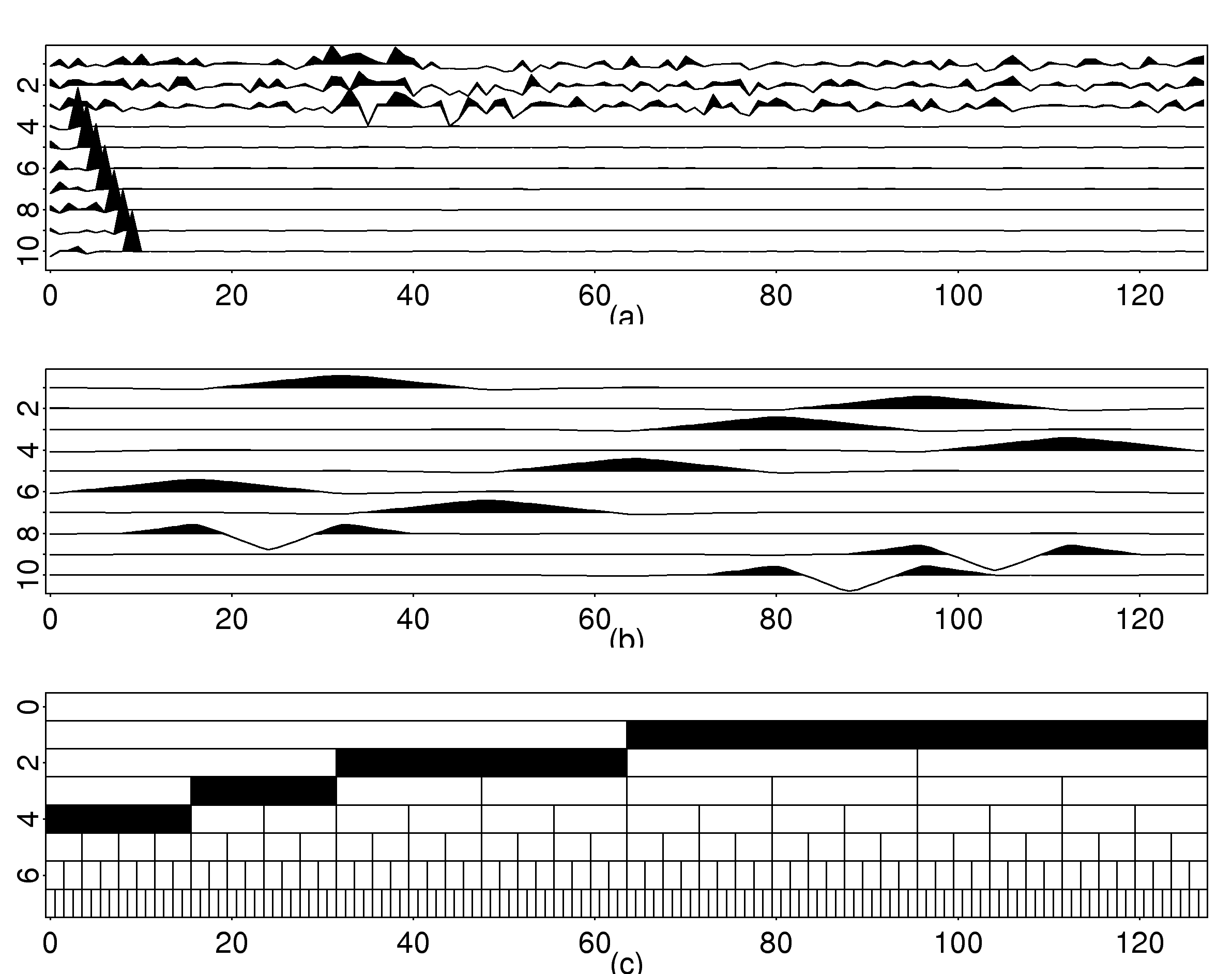
These three articles are picked out along with the Astronomy articles because they contain some astronomical keywords as one can see. Similarly, one can analyze another coarse block in Figure (c), which supports 62 documents: 56 of which are in Medical Sciences and the remaining six are non-medical articles that just happen to contain medical terms."Old Glory, New Glory: The Star-Spangled Banner gets some tender loving care" [Anthropology; on the preservation of the Star-Spangled Banner (flag) using the space-age technology]
"Snouts: A star is born in a very odd way" [Life Sciences; on star-nosed moles]
"Gravity tugs at the center of a priority battle" [Math/CS; on the priority war on the discovery of gravity between Newton, Halley, and Hooke]
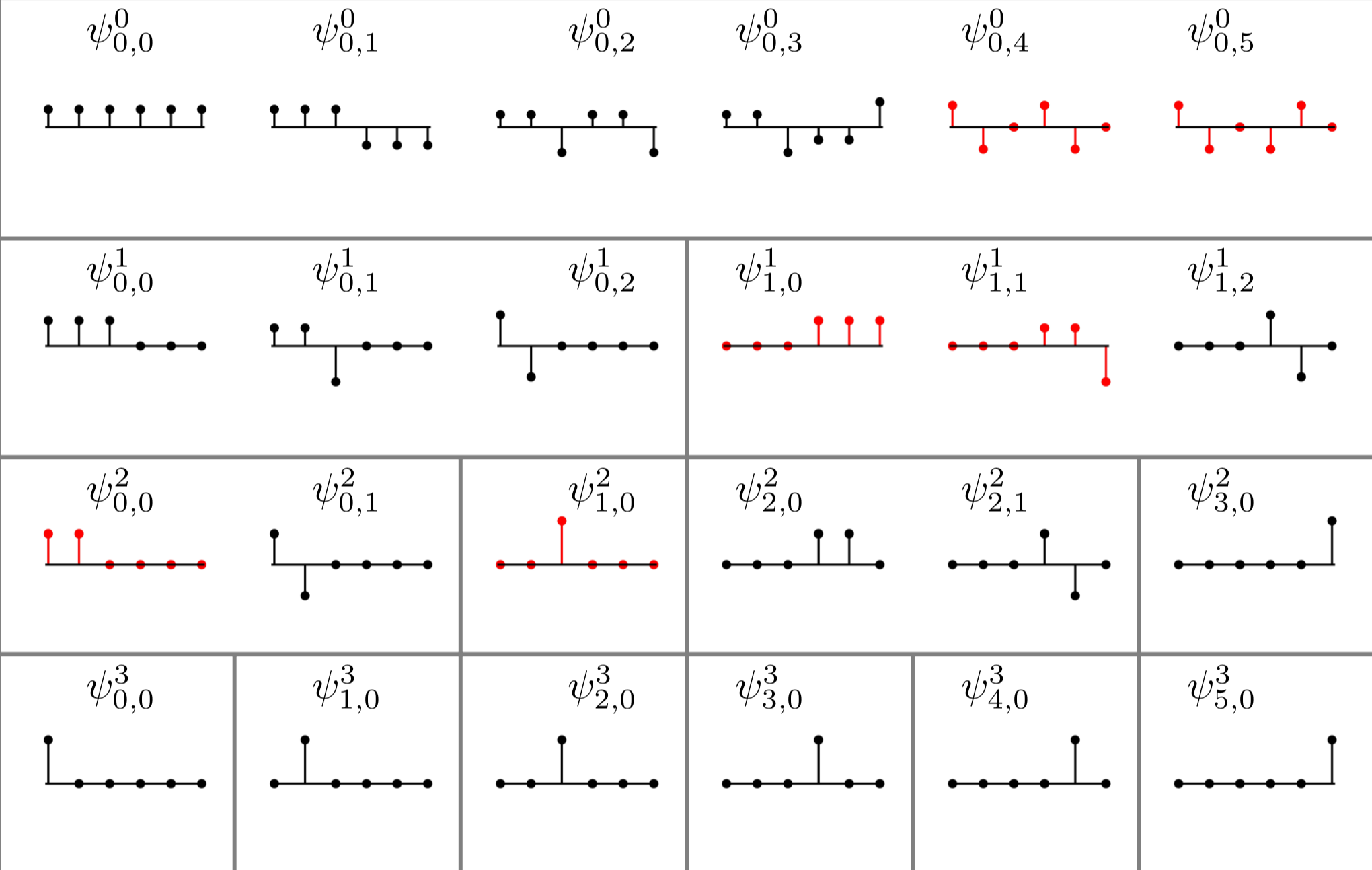



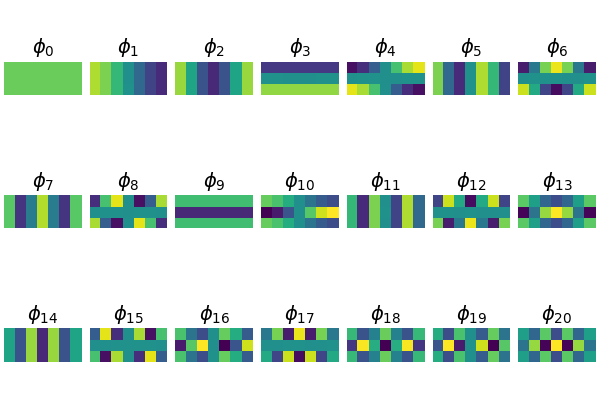
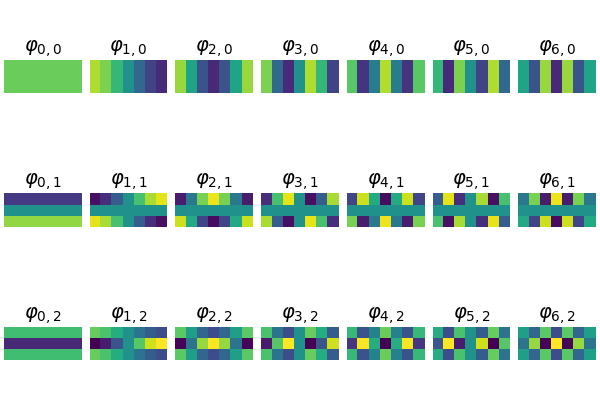
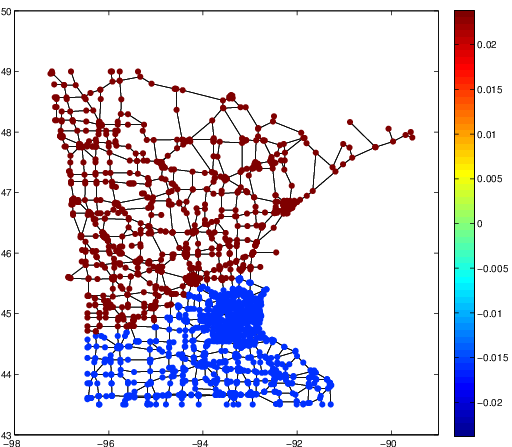
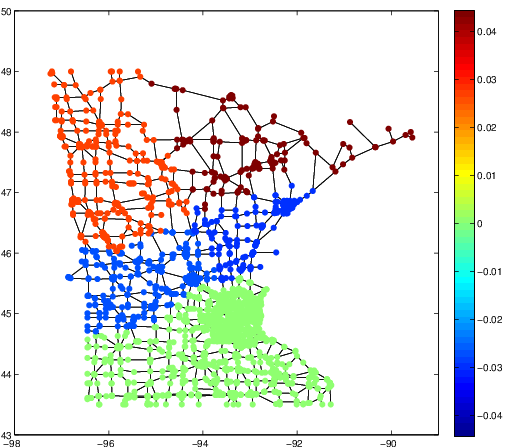
Given any two probability distributions \(p, q\) on a connected graph \(G(V,E,W)\) with graph geodesic distance metric \(d: V \times V \to \mathbb{R}_{\geq 0}\), $$ W_1(p,q) \leq K(p-q; \infty) \leq C \cdot W_1(p,q) , $$ where \(W_1(p,q) := \inf_{\gamma \in \Gamma(p,q)} \int_{V \times V} d(x,y) \, \mathrm{d}\gamma(x,y)\), \(\Gamma(p,q)\) denotes the collection of all measures on \(V\times V\) with marginals \(p\) and \(q\) in the first and second factors, respectively and \(C\) is a constant depends on \(G\).We managed to prove the first half of the conjecture so far, i.e., \(W_1(p,q) \leq K(p-q; \infty)\), but it is still a mystery about the explicit formulation of the constant \(C\) in second half.