Research - Anne Schilling

My research interests range from algebraic combinatorics, representation theory to mathematical physics. I have been interested in combinatorial properties of quantum algebras. Quantum algebras have their roots in two dimensional solvable lattice models in statistical mechanics. Kashiwara showed that at zero temperature the quantum algebras exhibit beautiful combinatorial properties. Mathematically these are formulated in the crystal base theory. Particularly nice crystals are Kirillov-Reshetikhin crystals; they are affine finite-dimensional crystals that can be used in the Kyoto path model to construct highest weight affine crystals. They are also in close relation to Demazure crystals as shown in work with Fourier and Shimozono. Together with Okado and Fourier, I showed that all Kirillov-Reshetikhin crystals of nonexceptional types exist and constructed them combinatorially exploiting certain automorphisms of the affine Dynkin diagrams. With Kirillov and Shimozono I have established a relation between crystal base theory and other combinatorial objects, called rigged configurations, which also arise from physics. A generalization of this result provides new fermionic formulas of the physical partition sums which, as follows by work of the Stony Brook group, encapture the statistics of the particle in the physics model (actually these statistics are similar to those found in the fractional quantum Hall effect; see here). In terms of q-series these yield generalizations of the famous Rogers-Ramanujan identities.

I have also worked on affine Schubert calculus and algebraic approaches using semigroup theory to Markov chains. Recently, with Brauner, Corteel and Daugherty, I have developed the new theory of crystal skeletons which provide a representation theoretic foundation for quasisymmetric functions.

I am especially fond of understanding relations between different areas in mathematics and mathematical physics. Often this helps to unravel hard problems in one area by exploiting the techniques of another area. I have also contributed to the open-source computer package Sage through Sage-Combinat by implementing crystal bases and Kirillov-Reshetikhin crystals (I previously contributed to MuPAD-Combinat). If you want to learn more on how to use crystals in Sage, there is a thematic tutorial on Lie methods and related combinatorics written in collaboration with Dan Bump from Stanford.

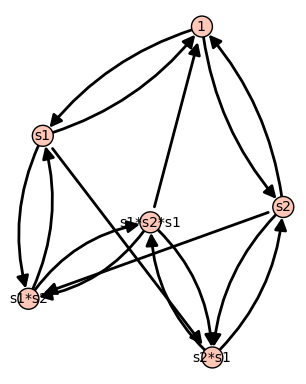
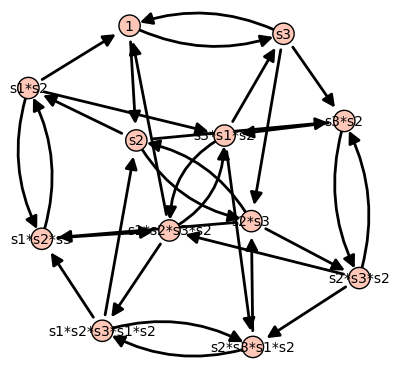
(Parabolic) quantum Bruhat graphs for A2 and A3 with J={1}

• q-Deformations of the Tsetlin library
  with Arvind Ayyer, Sarah Brauner, Jan de Gier
  preprint arXiv:2601.21195


• A geometric and generating function approach to plethysm
  with Alvaro Gutierrez, Rosa Orellana, Franco Saliola, Mike Zabrocki
  preprint arXiv:2511.02649


• Crystal skeletons: Combinatorics and axioms
  with Sarah Brauner, Sylvie Corteel, Zajj Daugherty
  preprint arXiv:2503.14782


• Crystal skeletons and their axioms
  with Sarah Brauner, Sylvie Corteel, Zajj Daugherty
  Seminaire Lotharingien de Combinatoire 93B (2025) #137, 12pp


• Complexity of finite semigroups: History and decidability
  with Stuart Margolis, John Rhodes
  Semigroup Forum (2025) https://doi.org/10.1007/s00233-025-10560-z ( arXiv:2501.00770 )


• Hook-valued tableau uncrowding and tableau switching
  with Jihyeug Jang, Jang Soo Kim, Jianping Pan, Joseph Pappe
  SIAM J. Discrete Mathematics 40 (1) (2026) 32-51 ( arXiv:2410.18343 )


• A hidden symmetry of refined canonical stable Grothendieck polynomials
  with Jihyeug Jang, Jang Soo Kim, Jianping Pan, Joseph Pappe
  Seminaire Lotharingien de Combinatoire 93B (2025) #18, 12pp


• Decidability of Krohn-Rhodes complexity for all finite semigroups and automata
  with Stuart Margolis, John Rhodes
  preprint arXiv:2406.18477


• The Combinatorial Theory flip
  Notices of the AMS 72 (1) (2025) 74-77


• The lattice of submonoids of the uniform block permutations containing the symmetric group
  with Rosa Orellana, Franco Saliola, Mike Zabrocki
  Semigroup Forum (2025) https://doi.org/10.1007/s00233-025-10505-6 ( arXiv:2405.09710 )


• The immersion poset on partitions
  with Lisa Johnston, David Kenepp, Evuilynn Nguyen, Digjoy Paul, Mary Claire Simone, Regina Zhou
  J. Alg. Combinatorics 61, 21 (2025) 61, 21 https://doi.org/10.1007/s10801-025-01380-z ( arXiv:2404.07393 )


• From quasi-symmetric to Schur expansions with applications to symmetric chain decompositions and plethysm
  with Rosa Orellana, Franco Saliola, Mike Zabrocki
  Electronic J. Comb. 31(4) (2024) #P4.23 ( arXiv:2404.04512 )


• Dimension of splines on graphs in the case of degree two and smoothness one in two variables
  with Shaheen Nazir, Julianna Tymoczko
  SIAM Journal on Applied Algebra and Geometry, to appear (arXiv:2309.11650)


• Promotion for fans of Dyck paths
  with Joseph Pappe, Stephan Pfannerer, Mary Claire Simone
  Seminaire Lotharingien de Combinatoire 89B (2023) Article #20, 12 pp


• Interview
  with Toufik Mansour
  ECA 3:2 (2023) Interview #S3I5 ( https://doi.org/10.54550/ECA2023V3S2I5 )


• Promotion and growth diagrams for fans of Dyck paths and vacillating tableaux
  with Joseph Pappe, Stephan Pfannerer, Mary Claire Simone
  J. Algebra 655 (2024) 1, 794-842 ( arXiv:2212.13588 )


• The mystery of plethysm coefficients
  with Laura Colmenarejo, Rosa Orellana, Franco Saliola, Mike Zabrocki
  Proceedings of Symposia in Pure Mathematics (PSPUM) 110 (2024), 275-292 ( arXiv:2208.07258 )


• The Burge correspondence and crystal graphs
  with Joseph Pappe, Digjoy Paul
  European J. Comb. 108 (2023) 103640 ( arXiv:2204.06751 )


• Plethysm and the algebra of uniform block permutations
  with Rosa Orellana, Franco Saliola, Mike Zabrocki
  Algebraic Combinatorics 5 (2022) 5, 1165-1203 ( arXiv:2112:13909 )


• Decidability of Krohn-Rhodes complexity c=1 of finite semigroups and automata
  with Stuart Margolis, John Rhodes
  preprint arXiv:2110.10373


• An area-depth symmetric q,t-Catalan polynomial
  with Joseph Pappe, Digjoy Paul
  Electronic J. Comb. 29(2) (2022), #P2.13 ( arXiv:2109.06300 )


• Uncrowding algorithm for hook-valued tableaux
  with Jianping Pan, Joseph Pappe, Wencin Poh
  Annals of Combinatorics 26 (2022), 261-301 ( arXiv:2012.14975 )


• Mixing time for Markov chain on linear extensions
  with John Rhodes
  Seminaire Lotharingien de Combinatoire 85B (2021) Article #27, 12 pp.


• Upper bounds on mixing time of finite Markov chains
  with John Rhodes
  SIAM J. on Discrete Mathematics 36(4) (2022), 3031-3057 ( arXiv:2010.08879 )


• Holonomy theorem for finite semigroups
  with John Rhodes, Pedro V. Silva
  International Journal of Algebra and Computation 32(3) (2022), 443-460 ( arXiv:2007.15552 )


• Markov chains through semigroup graph expansions (a survey)
  with John Rhodes
  Springer Proceedings in Mathematics & Statistics, vol 345. Springer, Singapore. ( arXiv:2006.00895 )


• A crystal on decreasing factorizations in the 0-Hecke monoid
  with Jennifer Morse, Jianping Pan, Wencin Poh
  Electronic J. Comb. 27(2) (2020), #P2.29 ( arXiv:1911.08732 )
  Crystal for Stable Grothendieck polynomials
  Seminaire Lotharingien de Combinatoire 84B (2020) Article #33, 12 pp


• Generalized q,t-Catalan numbers
  with Eugene Gorsky, Graham Hawkes, Anne Schilling, Julianne Rainbolt
  Algebraic Combinatorics 3(4) (2020) 855-886 ( arXiv:1905.10973 )


• An insertion algorithm on multiset partitions with applications to diagram algebras
  with Laura Colmenarejo, Rosa Orellana, Franco Saliola, Mike Zabrocki
  J. Algebra 557 no. 1, (2020), 97-128 ( arXiv:1905.02071 )
  An insertion algorithm for diagram algebras
  Seminaire Lotharingien de Combinatoire 84B (2020) Article #48, 12 pp


• Normal distributions of finite Markov chains
  with John Rhodes
  International Journal of Algebra and Computation 29, no. 8, (2019) 1431-1449 ( arXiv:1902.01042 )


• Queer supercrystals in SageMath
  with Wencin Poh
  Seminaire Lotharingien de Combinatoire 82B (2019) #102, 11pp


• Combinatorial characterization of queer supercrystals (survey)
  with Maria Gillespie, Graham Hawkes, Wencin Poh
  Bahar Acu et al. (eds.), Advances in Mathematical Sciences, Association for Women in Mathematics Series 21


• Characterization of queer supercrystals
  with Maria Gillespie, Graham Hawkes, Wencin Poh
  J. Combinatorial Theory, Series A 173 (2020) 105235 ( arXiv:1809.04647 )


• Unified theory for finite Markov chains
  with John Rhodes
  Advances in Mathematics 347 (2019) 739-779 ( arXiv:1711.10689 )


• A minimaj-preserving crystal on ordered multiset partitions
  with Georgia Benkart, Laura Colmenarejo, Pamela E. Harris, Rosa Orellana, Greta Panova, Martha Yip
  Advances in Applied Math. 95 (2018) 96-115 ( arXiv:1707.08709 )
  Seminaire Lotharingien de Combinatoire 80B (2018) #12, 12pp


• Rigged configuration bijection and proof of the X=M conjecture for nonexceptional affine types
  with Masato Okado and Travis Scrimshaw
  J. Algebra 516 (2018) 1-37 ( arXiv:1707.04876 )


• A Demazure crystal construction for Schubert polynomials
  with Sami Assaf
  Algebraic Combinatorics 1(2) (2018) 225-247 ( arXiv:1705.09649 )
  Erratum


• Crystal analysis of type C Stanley symmetric functions
  with Graham Hawkes and Kirill Paramonov
  Seminaire Lotharingien de Combinatoire 78B (2017) #8, 12 pp
  Electronic J. Comb. 24(3) (2017) #P3.51 ( arXiv:1704.00889 )


• Crystal Bases: Representations and Combinatorics
  with Daniel Bump
  World Scientific, 2017, ISBN: 978-981-4733-43-4, 292pp
  MAA review of the book!
  Errata


• Local limit of the fixed point forest
  with Tobias Johnson and Erik Slivken
  Electronic Journal of Probability 22 (2017), paper no. 18, 1-26 ( arXiv:1605.09777 [math.PR] )


• Affine crystals, Macdonald polynomials, and combinatorial models; extended abstract
  with Cristian Lenart, Satoshi Naito, Daisuke Sagaki, Mark Shimozono
  Rev. Roumaine Math. Pures Appl. 62 (2017), 1, 113-135


• The semaphore codes attached to a Turing machine via resets and their various limits
  with John Rhodes and Pedro V. Silva
  International Journal of Algebra and Computation 26(4) (2016) 675-704 ( arXiv:1604.00959 [math.GR] )


• Type D_n^{(1)} rigged configuration bijection
  with Masato Okado, Reiho Sakamoto, Travis Scrimshaw
  Journal of Algebraic Combinatoris 46 (2017) 341-401 ( arXiv:1603.08121 [math.QA] )


• A uniform model for Kirillov-Reshetikhin crystals III: Nonsymmetric Macdonald polynomials at t=0 and Demazure characters
  with Cristian Lenart, Satoshi Naito, Daisuke Sagaki, Mark Shimozono
  Transformation Groups 22(4) (2017) 1041-1079 ( arXiv:1511.00465 [math.QA] )


• Random walks on semaphore codes and delay de Bruijn semigroups
  with John Rhodes and Pedro V. Silva
  International Journal of Algebra and Computation 26(4) (2016) 635-673 ( arXiv:1509.03383 [math.GR] )


• Braid moves in commutation classes of the symmetric group
  with Nicolas M. Thiéry, Graham White, Nathan Williams
  European J. Combin. 62 (2017) 15-34 ( arXiv:1507.00656 [math.CO] )


• Explicit description of the degree function in terms of quantum Lakshmibai-Seshadri paths
  with Cristian Lenart, Satoshi Naito, Daisuke Sagaki, Mark Shimozono
  Toyama Math. Journal 37 (2015) 107-130 ( arXiv:1504.04707 [math.QA] )


• Affine charge and the k-bounded Pieri rule
  with Jennifer Morse
  DMCTS proc FPSAC'15 (2015) 405-416


• Spectral gap for random-to-random shuffling on linear extensions
  with Arvind Ayyer and Nicolas M. Thiery
  Experimental Math. 26(1) (2017) 22-30 ( arXiv:1412.7488 [math.PR] )


• Crystal structure on rigged configurations and the filling map
  with Travis Scrimshaw
  Electronic J. Combinatorics 22(1) (2015) #P1.73 ( arXiv:1409.2920 [math.CO] )


• Crystal approach to affine Schubert calculus
  with Jennifer Morse
  International Mathematics Research Notices 2016(8) (2016) 2239-2294 ( arXiv:1408.0320 [math.CO] )


• Richard Stanley through a crystal lens and from a random angle
  in: The Mathematical Legacy of Richard P. Stanley, AMS 2016, edited by P. Hersh, T. Lam, P. Pylyavskyy, V. Reiner, pp. 287-299 ( arXiv:1405.2966 [math.CO] )


• A uniform model for Kirillov-Reshetikhin crystals II. Alcove model, path model, and P=X
  with Cristian Lenart, Satoshi Naito, Daisuke Sagaki, and Mark Shimozono
  International Mathematics Research Notices 2017(14) (2017) 4259-4319 ( arXiv:1402.2203 [math.QA] )


• Markov chains, R-trivial monoids and representation theory
  with Arvind Ayyer, Benjamin Steinberg, and Nicolas M. Thiery
  International Journal of Algebra and Computation 25 (2015) 69-231 ( arXiv:1401.4250 [math.CO] )


• Flag Gromov-Witten invariants via crystals
  with Jennifer Morse
  DMTCS proc. AT (2014) 489-500


• Quantum Lakshmibai-Seshadri paths and root operators
  with Cristian Lenart, Satoshi Naito, Daisuke Sagaki, and Mark Shimozono
  Advanced Studies in Pure Mathematics (Mathematical Society of Japan, Tokyo) 71 (2016), Schubert Calculus - Osaka 2012, pp. 267-294 ( arXiv:1308.3529 [math.QA] )


• Markov chains for promotion operators
  with Arvind Ayyer and Steven Klee
  Fields Institute Communications 71 (2014) 285-304 (Springer) ( arXiv:1307.7499 [math.PR] )


• Directed nonabelian sandpile models on trees
  with Arvind Ayyer, Benjamin Steinberg, Nicolas M. Thiery
  Communications Math. Physics 335 (2015) 1065-1098 ( arXiv.1305.1697 [math.PR] )


• k-Schur functions and affine Schubert calculus
  with Thomas Lam, Luc Lapointe, Jennifer Morse, Mark Shimozono, and Mike Zabrocki
  Fields Institute Monographs 33 (Springer), ISBN 978-1-4939-0682-6 (eBook) ( arXiv.1301.3569 [math.CO] )


• A uniform model for Kirillov-Reshetikhin crystals. Extended abstract.
  with Cristian Lenart, Satoshi Naito, Daisuke Sagaki, and Mark Shimozono
  DMTCS proc AS (2013) 25-36 ( arXiv.1211.6019 [math.QA] )


• A uniform model for Kirillov-Reshetikhin crystals I: Lifting the parabolic quantum Bruhat graph
  with Cristian Lenart, Satoshi Naito, Daisuke Sagaki, and Mark Shimozono
  International Mathematics Research Notices 2015(7):1848-1901. ( arXiv.1211.2042 [math.QA] )


• Combinatorial Markov chains on linear extensions
  with Arvind Ayyer and Steven Klee
  J. Algebraic Combinatorics, 39(4) (2014) 853-881 ( arXiv:1205.7074 [math.CO] )


• A combinatorial formula for fusion coefficients
  with Jennifer Morse
  DMTCS proc AR (2012) 735-744 ( arXiv:1207.0786 [math.CO] )


• Affine crystal structure on rigged configurations of type D_n^(1)
  with Masato Okado and Reiho Sakamoto
  J. Algebraic Combinatorics, 37(3) (2013) 571-599 ( arXiv:1109.3523 [math.QA] )


• Crystal energy functions via the charge in types A and C
  with Cristian Lenart
  Mathematische Zeitschrift, 273(1) (2013) 401-426 ( arXiv:1107.4169 [math.CO] )
  DMTCS proc AR (2012) 9-20 (FPSAC version)


• Symmetric chain decomposition for cyclic quotients of Boolean algebras and relation to cyclic crystals
  with Patricia Hersh
  International Mathematics Research Notices 2013 (2) 463-473 ( arXiv:1107.4073 [math.CO] )


• Demazure crystals, Kirillov-Reshetikhin crystals, and the energy function
  with Peter Tingley
  The Electronic Journal of Combinatorics 19(2) (2012) P2 ( arXiv:1104.2359 [math.QA] )
  DMTCS proc AO (2011) 861-872 (FPSAC version)


• The biHecke monoid of a finite Coxeter group and its representations
  with Florent Hivert and Nicolas Thiery
  Algebra and Number Theory Journal 7(3) (2013) 595-671 ( arXiv:1012.1361 [math.CO] )


• On the representation theory of finite J-trivial monoids
  with Tom Denton, Florent Hivert, Nicolas Thiery
  Seminaire Lotharingien de Combinatoire, B64d (2011), 44 pp ( arXiv:1010.3455 [math.RT] )


• The Murnaghan-Nakayama rule for k-Schur functions
  with Jason Bandlow and Mike Zabrocki
  Journal of Combinatorial Theory, Series A, 118(5) (2011) 1588-1607 ( arXiv:1004.4886 [math.C0] )
  DMTCS proc AO (2011) 99-110 (FPSAC version)
  Oberwolfach Report


• The biHecke monoid of a finite Coxeter group
  with Florent Hivert and Nicolas Thiery
  DMTCS proc AN (2010) 307-318 ( arXiv:0912.2212 [math.CO] )


• Affine structures and a tableau model for E_6 crystals
  with Brant Jones
  J. Algebra 324 (2010) 2512-2542 ( arXiv:0909.2442 [math.CO] )
  DMTCS proc AN (2010) 785-796 (FPSAC version)


• Promotion operator on rigged configurations of type A
  with Qiang Wang
  The Electronic Journal of Combinatorics 17 Issue 1 (2010) R24 ( arXiv:0908.2458 [math.CO] )


• K-theory Schubert calculus of the affine Grassmannian
  with Thomas Lam and Mark Shimozono
  Compositio Mathematica 146 Issue 4 (2010) 811-852 ( arXiv:0901.1506 [math.CO] )


• Perfectness of Kirillov-Reshetikhin crystals for nonexceptional types
  with Ghislain Fourier and Masato Okado
  Contemp. Math. 506 (2010) 127-143 ( arXiv:0811.1604 [math.RT] )
  DMTCS proc AK (2009) 426-439 (FPSAC version)


• Kirillov-Reshetikhin crystals for nonexceptional types
  with Ghislain Fourier and Masato Okado
  Advances in Mathematics 222 Issue 3 (2009) 1080-1116 ( arXiv:0810.5067 [math.RT] )


• On the uniqueness of promotion operators on tensor products of type A crystals
  with Jason Bandlow and Nicolas Thiery
  J. Algebraic Combinatorics 31 (2010) 217-251 ( arXiv:0806.3131 [math.CO] )


• Hecke group algebras as quotients of affine Hecke algebras at level 0
  Journal of Combinatorial Theory, Series A 116 (2009) 844-863 ( arXiv:0804.3781 [math.RT] )
  Hecke group algebras as degenerate affine Hecke algebras
  DMTCS proc AJ (2008) 611-624
  with Florent Hivert and Nicolas Thiery


• Schubert Polynomials for the affine Grassmannian of the symplectic group
  with Thomas Lam and Mark Shimozono
  Mathematische Zeitschrift 264(4) (2010) 765-811 ( arXiv:0710.2720 [math.CO] )


• The forgotten monoid
  with Jean-Christophe Novelli
  RIMS Kokyuroku Bessatsu B8 (2008) 71-83 ( arXiv:0706.2996 [math.CO] )


• Existence of Kirillov-Reshetikhin crystals for nonexceptional types
  with Masato Okado
  Representation Theory 12 (2008) 186-207 ( arXiv:0706.2224 [math.QA] )


• Combinatorial structure of Kirillov-Reshetikhin crystals of type D_n(1), B_n(1), A_{2n-1}(2)
  J. Algebra 319 (2008) 2938-2962 ( arXiv:0704.2046 [math.QA] )


• Demazure structure inside Kirillov-Reshetikhin crystals
  with Ghislain Fourier and Mark Shimozono
  J. Algebra 309 (2007) 386-404 ( math.QA/0605451 )


• X=M Theorem: Fermionic formulas and rigged configurations under review
  MSJ Memoirs 17 (2007) 75-104 (published by the Mathematical Society of Japan) ( math.QA/0512161 )


• Virtual crystal structure on rigged configurations
  Formal Power Series and Algebraic Combinatorics, San Diego, California 2006 ( pdf file )


• New fermionic formula for unrestricted Kostka polynomials
  with Lipika Deka
  J. Combinatorial Theory, Series A 113 (2006) 1435-1461 ( math.CO/0509194 )


• Crystal structure on rigged configurations
  International Mathematics Research Notices, Volume 2006, Article ID 97376, Pages 1-27 ( math.QA/0508107 )


• Non-unitary minimal models, Bailey's lemma and N=1,2 superconformal algebras
  with Lipika Deka
  Commun. Math. Phys. 260 (2005) 711-725 ( math-ph/0412084 )


• X=M for symmetric powers
  with Mark Shimozono
  J. Algebra 295 (2006) 562-610 ( math.QA/0412376 )


• A simple introduction to crystals B^{2,s} for Kirillov-Reshetikhin modules of type D_n^{(1)}
  with Philip Sternberg
  in: A. Kuniba, M. Okado (Eds.), RIMS Kokyuroku 1429 "Combinatorial Aspect of Integrable Systems", to appear. ( postscript file )


• Finite-dimensional crystals B^{2,s} for quantum affine algebras of type D_n^{(1)}
  with Philip Sternberg
  J. Alg. Combin. 23 (2006) 317-354 ( math.QA/0408113 )


• A bijection between type D_n^{(1)} crystals and rigged configurations
  J. Algebra 285 (2005) 292-334 ( math.QA/0406248 )
  Supplementary Notes


• Rigged configurations and the Bethe Ansatz
  in: B. Lulek, T. Lulek and A. Wal (Eds), "Symmetry and Structural Properties of Condensed Matter", Vol. 7, World Scientific, Singapore 2003; pp. 201-224 ( math-ph/0210014 )


• Virtual crystals and Kleber's algorithm
  with Masato Okado and Mark Shimozono
  Commun. Math. Phys. 238 (2003) 187-209 ( math.QA/0209082 )


• A crystal to rigged configuration bijection for nonexceptional affine algebras
  with Masato Okado and Mark Shimozono
  "Algebraic Combinatorics and Quantum Groups", Edited by N. Jing, World Scientific (2003), 85-124 ( math.QA/0203163 )


• A tensor product theorem related to perfect crystals
  with Masato Okado and Mark Shimozono
  J. Algebra 267 (2003) 212-245 ( math.QA/0111288 )


• q-Supernomial coefficients: From riggings to ribbons
  in: MathPhys Odyssey 2001, M. Kashiwara and T. Miwa (eds.), Birkhaeuser Boston, Cambridge, MA, 2002, pp. 437-454 ( math.CO/0107214 )


• Virtual crystals and fermionic formulas of type $D_{n+1}^{(2)}$, $A_{2n}^{(2)}$, and $C_n^{(1)}$
  with Masato Okado and Mark Shimozono
  Representation Theory 7 (2003) 101-163 ( math.QA/0105017 )


• Crystal bases and q-identities
  with Masato Okado and Mark Shimozono
  Contemp. Math. 291 (2001) 29-53 ( math.QA/0104268 )


• Branching formula for q-Littlewood--Richardson coefficients
  with Mark Shimozono and Dennis E. White
  Advances in Applied Mathematics 30 (2003) 258-272 ( postscript file )


• Fermionic formulas for level-restricted generalized Kostka polynomials and coset branching functions
  with Mark Shimozono
  Commun. Math. Phys. 220 (2001) 105-164 ( math.QA/0001114 )


• New expressions for level-restricted Kostka polynomials
  with Mark Shimozono
  in: Formal Power Series and Algebraic Combinatorics, D. Krob, A.A. Mikhalev, A.V. Mikhalev (eds.), 12th International conference, FPSAC'00, Moscow, Russia, June 2000, Proceedings, Springer Verlag Berlin/Heidelberg 2000, pp. 367-378. ( postscript file )


• A generalization of the $q$-Saalschütz sum and the Burge transform
  with S. Ole Warnaar
  in: Physical Combinatorics, M. Kashiwara and T. Miwa (eds.), Birkhaeuser Boston, Cambridge, MA, 2000, pp. 163-183. ( math.QA/9909044 )


• Conjugate Bailey pairs. From configuration sums and fractional-level string functions to Bailey's lemma
  with S. Ole Warnaar
  Contemp. Math. 297 (2002) 227-255 ( math.QA/9906092 )


• A bijection between Littlewood-Richardson tableaux and rigged configurations
  with Anatol N. Kirillov and Mark Shimozono
  Selecta Mathematica (N.S.) 8 (2002) 67-135 ( math.CO/9901037 )


• Various representations of the generalized Kostka polynomials
  with Anatol N. Kirillov and Mark Shimozono
  Seminaire Lotharingien de Combinatoire 42 [B42j] (1999) ( postscript file )


• Bosonic formula for level-restricted paths
  with Mark Shimozono
  Advanced Studies in Pure Mathematics 28, Combinatorial Methods in Representation Theory (2000) 305-325 ( math.QA/9812106 )


• An A$_2$ Bailey lemma and Rogers-Ramanujan-type identities
  with George E. Andrews and S. Ole Warnaar
  J. Amer. Math. Soc. 12 (1999) 677-702 ( math.QA/9807125 )


• Inhomogeneous lattice paths, generalized Kostka polynomials and A$_{n-1}$ supernomials
  with S. Ole Warnaar
  Commun. Math. Phys. 202 (1999) 359-401 ( math.QA/9802111 )


• Bailey flows and Bose-Fermi identities for the conformal coset models $(A_1^{(1)})_N\times (A_1^{(1)})_{N'}/(A_1^{(1)})_{N+N'}$
  with Alexander Berkovich, Barry M. McCoy, and S. Ole Warnaar
  Nucl. Phys. B499 [PM] (1997) 621-649 ( hep-th/9702026 )


• Supernomial coefficients, polynomial identities and $q$-series
  with S. Ole Warnaar
  The Ramanujan Journal 2 (1998) 459-494 ( q-alg/9701007 )


• Rogers-Schur-Ramanujan Type Identities for the $M(p,p')$ minimal models of Conformal Field Theory
  with Alexander Berkovich and Barry M. McCoy
  Commun. Math. Phys. 191 (1998) 325-395 ( q-alg/9607020 )


• A Higher-Level Bailey Lemma: Proof and Application
  with S. Ole Warnaar
  The Ramanujan Journal 2 (1998) 327-349 ( q-alg/9607014 )


• A Higher-level Bailey Lemma
  with S. Ole Warnaar
  Int. J. of Mod. Phys. B11 (1997) 189-195 ( q-alg/9604015 )


• $N=2$ Supersymmetry and Bailey Pairs
  with Alexander Berkovich and Barry M. McCoy
  Physica A 228 (1996) 33-62 ( hep-th/9512182 )


• Multinomials and Polynomial Bosonic Forms for the Branching Functions of the $\widehat{su}(2)_M \times \widehat{su}(2)_N / \widehat{su}(2)_{M+N}$ Conformal Coset Models
  Nucl. Phys. B467 (1996) 247-271 ( hep-th/9510168 )


• Polynomial Fermionic Forms for the Branching Functions of the Rational Coset Conformal Field Theories $\widehat{su}(2)_M \times \widehat{su}(2)_N / \widehat{su}(2)_{M+N}$
  Nucl. Phys. B459 (1996) 393-436 ( hep-th/9508050 )


• Multiplicative BRST renormalization of the $SU(2)$ Higgs model
  with Peter van Nieuwenhuizen
  Phys. Rev. D50 (1994) 967-970 ( hep-th/9408125 )

Comments and questions are welcome: aschilling@ucdavis.edu

Back to main homepage