Course Information

Lectures: Tuesdays and Thursdays 2:10-3:30pm at MSB 3106.

Syllabus: The course syllabus contains the basic guidelines for the course.

Office Hours: Tuesdays 3:30-4pm and Thursdays 3:30-4:30pm. Always feel free to ask before class or reach out for an appointment.

Important Dates: First Day (Sep 23), Veterans Day (Nov 11), Thanksgiving (Nov 25), Last Day (Dec 2).

Problem Sets: Weekly assignments are due on Fridays at 5:00pm, to be submitted through Gradescope.

Schematic depiction of an area of research within contact and symplectic topology:

Problem Sets

1. Problem Set 1: Due Friday Oct 1 and available Thu Sep 24. (TeX File PSet1).
   
   
2. Problem Set 2: Due Friday Oct 8 and available Friday Oct 1. (TeX File PSet2).
   
   
3. Problem Set 3: Due Friday Oct 15 and available Thu Oct 7. (TeX File PSet3).
   
   
4. Problem Set 4: Due Friday Oct 22 and available Friday Oct 15. (TeX File PSet4).
   
   
5. Problem Set 5: Due Friday Oct 29 and available Friday Oct 22. (TeX File PSet5).
   
   
6. Problem Set 6: Due Friday Nov 12 and available Saturday Nov 6. (TeX File PSet6).
   
   

Final Projects

1. Invariance of the category of sheaves associated to a Legendrian: There are two natural approaches in the case of Legendrian links. First, the original intrinsic geometric approach of [GKS] , which works in any dimension. This is the correct general way that conceptually explains why this categories are invariant under Legendrian isotopies. The reference [G19] and this working group can be a good additional resource. Second, the combinatorial approach of [STZ], which works just for Legendrian links in 3-dimensions. It is more elementary and enlightening from the perspectives of fronts diagrams.
   
   
2. The evolutions of optical wavefronts: This includes any project related to properties of Legendrian fronts that appear in geometric optics (systems of rays). Beautiful theorems include the Chekanov-Pushkar resolution of Arnold's 4-cusp conjecture [CP05] , which is combinatorial, and Guillermou's resolution of the 3-cusp conjecture [G16], which uses sheaf theory. (See also [G19].)
   
   
3. A study of the Cayley caustic: This project concerns the singularities (called caustics) developed by an ellipsoid under the inwards equidistant flow, which is the Reeb flow according to the contact interpretations of the Huygens' principle. The one-dimensional version is depicted in Figure 6 of [C21]. This two-dimensional version, with an ellipsoidal source of light, relates to Jacobi's Last Geometric Theorem. See also Sinclair's beautiful pictures in [S03]
   
   
4. Generating Family Homology: This project is about defining invariants of Legendrian links by using associated generating families [FR10]. Some good sources are [T01], [JT06], [L18] and [CH16]. The ingredients involved include the study of generating families, their sublevel sets and homology. A possible option is to relates this to ruling diagrams and augmentations, as in [HR16] and [HR13].
   
   
5. The moduli of sheaves microlocally supported on a cone: This project is about studying a particular front diagram in three-dimensions, and computing the spaces of sheaves whose microlocal support coincides with that front. This relates to the ellipse and ellipsoid front eversions, obtained by perturbing a spherical wavefront collapse.
   
   
6. The Thurston-Bennequin Inequality: This project concerns an upper bound of the Thurston-Bennequin invariant of a Legendrian link in the standard (tight) contact structure of 3-space. Two resources are [Section 5.2,E02] and [Section 3.1,E04] and references therein. A consequence of this inequality is that an overtwisted contact structurein 3-space is not contactomorphic to the standard contact structure.
   
   
7. The parallel parking problem (and ice skating): This project aims at filling in all the details to explain how contact geometry and Legendrian fronts naturally appear in problems related to control theory, such as the parallel parking problem. Relations with the theory of foliations and holonomic systems, as well as similar mechanical problems (such as the rolling penny) and Engel structures are also an option.
   
   
8. Microlocal support in relation to the study of linear PDEs: A possible goal is to relate Sato's notion of microlocal support of a sheaf with Hormander's notion of wavefront of a distribution. From the perspective of PDEs, it can be interesting to discuss the Cauchy-Kovalevskaya theory from a sheaf viewpoint, or explore the vanishing locus of the principal symbol through the microlocal support of a complex of sheaves. A detour in the theory of hypergeometric functions is also an option.
   
   
9. The Morse Lemma from the sheaf viewpoint: This aims at understanding that the topology of the sublevel sets of a Morse function change only a critical points, and in a specific manner, now in the presence of a sheaf. See [G19], notes from this working group, and reference therein.
   
   
10. Counting Morse functions on surfaces: This project aims at counting Morse functions on the 2-sphere, following [N08], whose asymptotics are studied in [N06]. Related references are [A06], [CG17], and se also [A07] and [Ar06].
    
    

Math Diaries

1. Thursday Sep 23: Introduction to MAT-280.
   
   Definition of a contact structure. Depiction of a 2-plane distribution.
   Vector fields and 1-forms. Parallel parking problem in terms of geometry.
   Allowed velocities and Legendrian arcs. Possibility of parallel parking.
   Definition of integral distribution. Statement of Frobenius Theorem.
   
   Additional: Read Section 2 in "Lectures on Contact Geometry in Low-Dimensional Topology" by J. Etnyre.
   See also the first six slides here.
   
   
2. Tuesday Sep 28: The Darboux Theorem and Isomorphism Notions.
   
   Examples of contact structures: using the Frobenius Integrability Theorem.
   Deformations of Contact Structures and Contactomorphism. Gray's Stability and Examples.
   Classification Problems: Constructions and Invariants. (Brief digression and comparisons.)
   Darboux Theorem: Non-existence of local invariants. A proof of the Darboux Theorem.
   
   Additional: See Massot's Gallery I for computer depictions of contact structure.
   See Massot's Gallery II for a deformation of (standard) contact structures.
   Another proof of the Darboux Theorem, Gray's Lemma is also proven there.
   
   
3. Thursday Sep 30: Legendrian knots.
   
   Smooth knots and smooth isotopies. Examples.
   Legendrian knots and Legendrian isotopies. Examples.
   Front projection for Legendrian knots: cusp and crossing models.
   From a Legendrian front to a smooth knot diagram.
   
   Additional: Gallery of Legendrian Knots.
   
   
4. Tuesday Oct 5: Legendrian knots II.
   
   Review of fronts and examples. Possible local singularities in a Legendrian front.
   The Legendrian realization theorem. Examples of knots up to five crossings. Proof of the theorem.
   Closeness of approximation. The Legendrian Reidemeister theorem. Examples of front isotopies.
   
   Additional: This lecture contained a discussion on regular knot diagrams.
   See Section 2.3 of Legendrian and Transversal Knots
   
   
5. Thursday Oct 7: Formal Legendrian Invariants.
   
   Review and plan. Definition of writhe. Thurston-Bennequin Invariant: Definition and Examples.
   Rotation number: Definition and examples. Invariance of (tb,r). Distinct Legendrians in same smooth type.
   Positive and Negative Stabilizations: Definition and effect on (tb,r). The Fuchs-Tabachnikov Theorem.
   
   Additional: After lecture, we discussed a differential topology proof of the smooth Reidemeister theorem.
   
   
6. Tuesday Oct 12: Generating Functions I.
   
   The Chekanov pair: two distinct Legendrian representatives of m(5₂) with the same formal invariants.
   The Legendrians in the Chekanov pair are Legendrian isotopic after one stabilization: proof by Reidemeister moves.
   Comment on simplicity for the unknot, 3₁ and 4₁ (using techniques from convex surfaces), and disparity for twist knots.
   Bird's Eye view on modern invariants: Generating functions, Legendrian Contact dg-algebra and constructible sheaves.
   Definition of a Generating Family. Example for the saucer front of the standard unknot.
   A peak into the future: a constructible sheaf associated to a generating family.
   
   
7. Thursday Oct 14: Generating Functions II.
   
   Generating family associated to the max-tb right-handed trefoil.
   Behavior of generating families under the Legendrian Reidemeister I Move.
   Stabilization of generating families: the need to increase domain dimension.
   Maslov potentials of Legendrian front. Connection between Maslov and Morse indices.
   Sublevel sets of a generating families and intersections with the projection fibers.
   
   
8. Tuesday Oct 19: Sheaves of complexes of vector spaces.
   
   From generating families to sheaves: assigning an Abelian group to each open stratum of the front complement.
   Intuition: the stalk record the cellular cohomology of the sublevel sets intersected with the projection fibers.
   Definition of a pre-sheaf and a sheaf. Examples of sheaves of different types of functions. Direct image sheaf.
   Pull-back sheaf. The étalé viewpoint of sheaf sections. What does a sheaf know about a space?
   
   
9. Thursday Oct 21: Cohomology of Sheaves.
   
   Open covers and good covers. Cech cohomology of the circle for the constant sheaf. The Cech differential.
   Intuition for the Cech differential, Cech co-chains and co-boundaries. Definition of Cech cohomology.
   Direct limits on the covers and computational importance of good covers. Gallery of examples and computations.
   Flabby sheaves and acyclicity. Examples and non-examples of flabby sheaves. Cohomology of sky-scraper sheaves.
   Cohomology of direct images on closed subsets. Cohomology of the constant sheaf for a genus-g surface.
   
   
10. Tuesday Oct 26: Singular Support of a Sheaf I.
    
    The art of studying first derivatives. The contact boundary of a cotangent bundle.
    Ice-skating and driving examples as Legendrian fronts. Co-normal lifts of planar fronts.
    Sheaf propagation. Definition of singular support of a sheaf. Examples on the real line.
    Examples of singular supports of direct images of constant sheaves on closed and open subsets.
    Properties of the singular support. The singular support of the sheaf of smooth functions.
    
    
11. Thursday Oct 28: Singular Support of a Sheaf II.
    
    Example of a sheaf whose singular support is contained in the Legendrian unknot.
    Issues that appear in the case of the max-tb Legendrian trefoil: singular support at crossings.
    Theorem A: Combinatorial description of sheaves with singular support contained in a front.
    Theorem B: The category of sheaves with singular support at a Legendrian is an invariant.
    The notion of a sheaf kernel and Guillermou-Kashiwara-Schapira quantization of isotopies.
    
    
12. Tuesday Nov 2: Proof of the combinatorial description.
    
    Regular stratifications. Stratification associated to a front. The poset category of a stratification.
    Generization maps associated to a constructible sheaf. Functor from sheaves to (the dual of) stratifications.
    Proof of Theorem A: Combinatorial description of sheaves with singular support contained in a front.
    The required acyclicity and quasi-isomorphism conditions at an arc, at a cusp and a crossing.
    
    
13. Thursday Nov 4: Sample Applications of the moduli of sheaves of Legendrians.
    
    Application I: distinguishing the Chekanov pair of two distinct Legendrian representatives of m(5₂).
    Application II: the 4-cusp theorem. Evolution of wavefronts: Huygens-Fresnel principle and sending waves.
    Application III: studying exact Lagrangian fillings of a Legendrian link, up to Hamiltonian isotopy.
    Application IV: the group of contactomorphisms is C⁰-closed in the group of diffeomorphisms.
    
    
14. Tuesday Nov 9: Computations of the moduli of sheaves of Legendrians.
    
    
15. Tuesday Nov 16: Lagrangian Fillings and their associated sheaves.
    
    
16. Thursday Nov 18: Infinitely many Lagrangian fillings distinguished by sheaves.
    
    

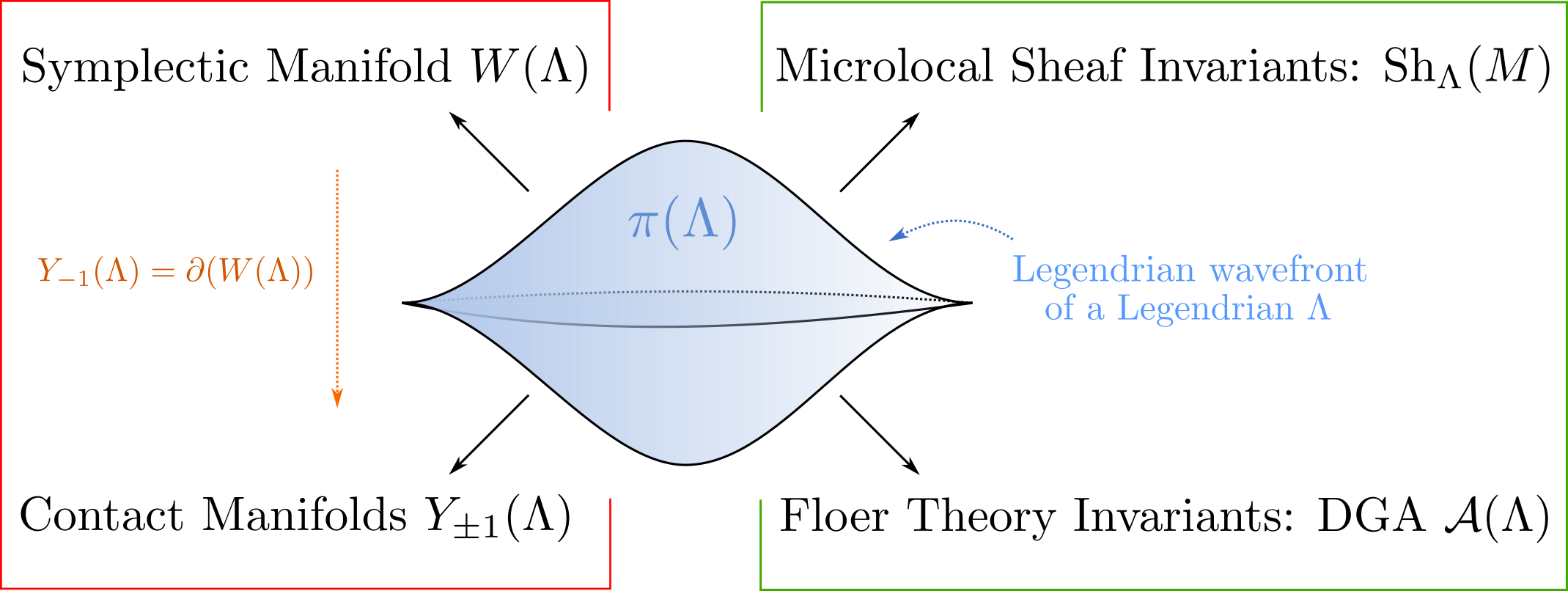
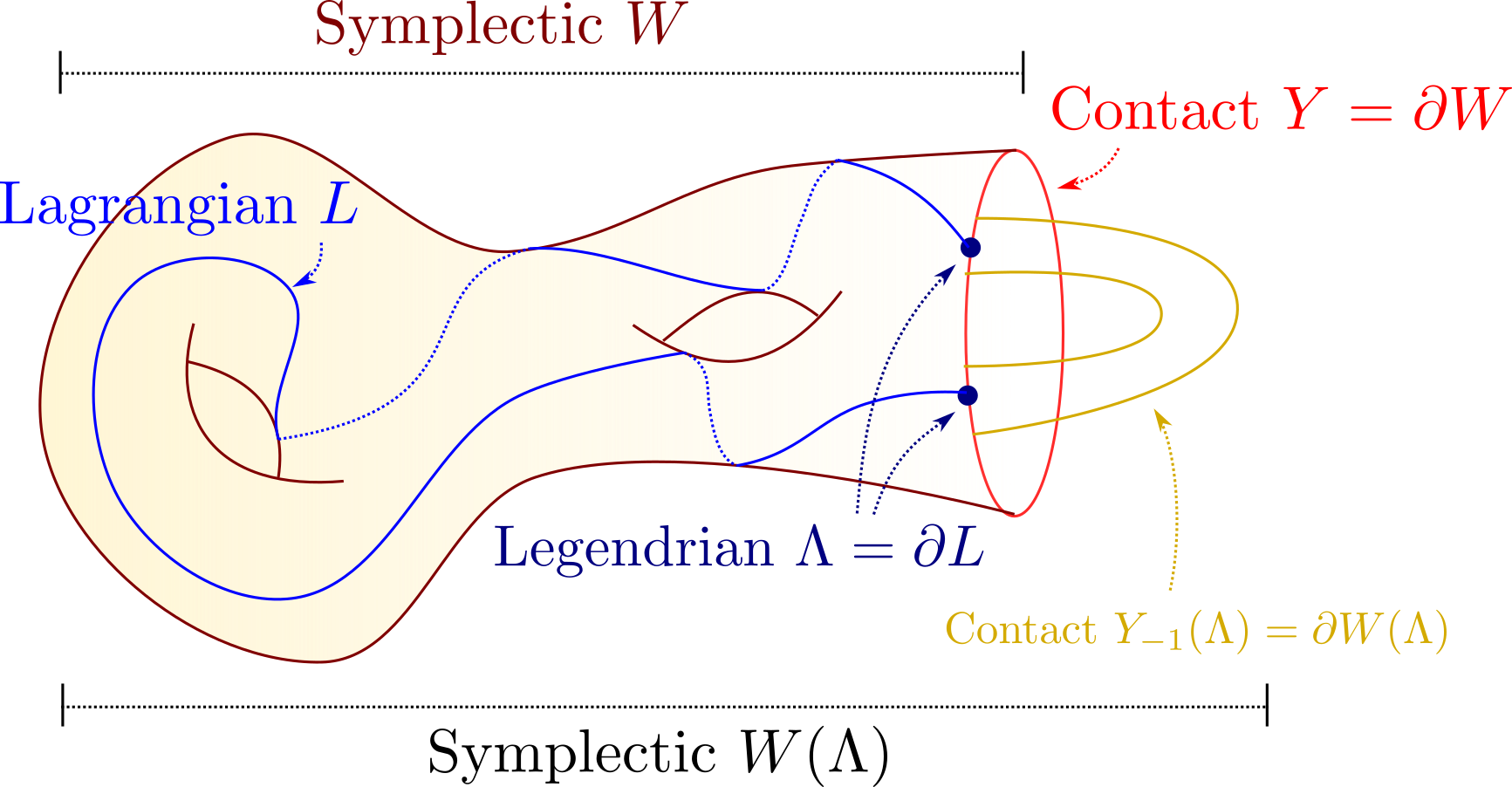
Further Resources

Introductory Texts on Contact and Symplectic Topology: Symplectic Geometry (Dynamical Systems IV), by V.I. Arnold and A. Givental, Singularities of Caustics and Wave Fronts and Mathematical Methods of Classical Mechanics (especially Appendix IV), both by V.I. Arnold, An Introduction to Contact Topology by H. Geiges.

Notes on Contact and Symplectic Topology: "Legendrian and Transversal Knots", "Introductory Lectures on Contact Geometry" and "Lectures on Contact Geometry in Low-Dimensional Topology" by J. Etnyre, "Topological methods in 3-dimensional contact geometry" (especially Chapter I) by P. Massot, "Contact geometry" by H. Geiges, "Contact geometry in 3 dimensions" by S. Sivek, "Contact Geometry Course" by K. Honda.

Graduate Textbooks on Contact and Symplectic Topology: Standard sources in the topic, more focused on symplectic topology include " Lectures on Symplectic Geometry", "Introduction to Symplectic Topology" by D. McDuff and D. Salamon, "Morse Theory and Floer Homology" by M. Audin and M. Damian, and "Surgery on Contact 3-Manifolds and Stein Surfaces" by B. Ozbagci and A. Stipsicz.

Textbooks on Smooth Topology: It is useful to be proficient in smooth topology when researching in contact and symplectic topology. Some useful sources for differential topology are "Morse Theory" by J. Milnor, "4-Manifolds and Kirby Calculus" by A. Stipsicz and R. Gompf, "Knots and Links" by D. Rolfsen, "Topological Methods in Algebraic Geometry" by F. Hirzebruch, and Low Dimensional Topology at PCMS.

Video resources: "41st Spring Lecture Series" by J. Etnyre (4 lectures), the " MSRI Summer Graduate Workshop" on Symplectic and Contact Geometry and Topology has about 30 lectures, from many experts and different viewpoints, such as J. Etnyre, M. Symington, L. Ng, D. McDuff and others, "An overview of Contact and Symplectic Topology" by P. Massot. "IMPA School of Symplectic Topology" has several introductory video lectures.