Homology of torus (and other) knots: what do we know?

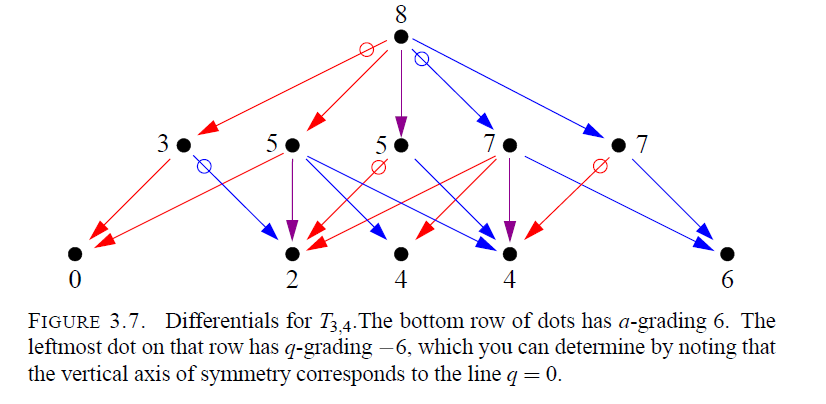
We plan to discuss recent progress in understanding HOMFLY-PT homology of torus links, and related algebro-geometric models. The main goal is to orient the audience (and the speakers) in the existing literature, and get a clear understanding of the status of various conjectures.

Picture credit: [DGR]
Contact: Eugene Gorsky
The seminar meets tentatively on Wednesdays at 9-10am US Pacific time= 12-1 US Eastern time = 6pm Central European Time.

Schedule

3/31 Introduction, definition of HOMFLY homology, y-ification [KhS,GH] notes

4/7 Explicit computations: recursions, full twist [H,HM,GH] notes

4/14 Guest lecture: Anton Mellit notes

4/21 Anton continues notes

4/8 Singular curves: Hilbert schemes, affine Springer fibers [ORS,Hik,GM,GMV2] notes

5/5 Guest lecture: Oscar Kivinen [K] notes

5/12 Guest lecture: Pavel Galashin [GL,GL2] typed notes , handwritten notes .

5/19 Banff workshop

5/26 Braid varieties [MChar,CGGS,CGGS2] notes

6/2 Hilb(C^2): overview [Hai,GNR,OR] notes

Bibliography

Soergel bimodules and HOMFLY-PT homology:

[KhS] M. Khovanov. Triply-graded link homology and Hochschild homology of Soergel bimodules. Internat. J. Math. 18 (2007), no. 8, 869-885.

[DGR] N. Dunfield, S. Gukov, J. Rasmussen. The superpolynomial for knot homologies. Experiment. Math. 15 (2006), no. 2, 129-159.

[H] M. Hogancamp. Categorified Young symmetrizers and stable homology of torus links. Geom. Topol. 22 (2018), no. 5, 2943-3002.

[HM] M. Hogancamp, A. Mellit. Torus link homology. arXiv:1909.00418

[GH] E. Gorsky, M. Hogancamp. Hilbert schemes and y-ification of Khovanov-Rozansky homology.arXiv:1712.03938

[GHM] E. Gorsky, M. Hogancamp, A. Mellit. Tautological classes and symmetry in Khovanov-Rozansky homology. arXiv:2103.01212

Singular curves:

[Hik] T. Hikita. Affine Springer fibers of type A and combinatorics of diagonal coinvariants. Adv. Math. 263 (2014), 88-122.

[ORS] A. Oblomkov, J. Rasmussen, V. Shende. The Hilbert scheme of a plane curve singularity and the HOMFLY homology of its link. Geom. Topol. 22 (2018), no. 2, 645-691.

[MY] D. Maulik, Z. Yun. Macdonald formula for curves with planar singularities. J. Reine Angew. Math. 694 (2014), 27-48.

[OY] A. Oblomkov, Z. Yun. Geometric representations of graded and rational Cherednik algebras. Adv. Math. 292 (2016), 601-706.

[K] O. Kivinen. Unramified affine Springer fibers and isospectral Hilbert schemes. Selecta Math. (N.S.) 26 (2020), no. 4, Paper No. 61, 42 pp.

[GM] E. Gorsky, M. Mazin. Compactified Jacobians and q,t-Catalan numbers, I. J. Combin. Theory Ser. A 120 (2013), no. 1, 49-63.

[GMV] E. Gorsky, M. Mazin, M. Vazirani. Affine permutations and rational slope parking functions. Trans. Amer. Math. Soc. 368 (2016), no. 12, 8403-8445.

[GMV2] E. Gorsky, M. Mazin, M. Vazirani. Recursions for rational q,t-Catalan numbers. J. Combin. Theory Ser. A 173 (2020), 105237, 28 pp.

Braid varieties:

[MChar] A. Mellit. Cell decompositions of character varieties. arXiv:1905.10685

[GL] P. Galashin, T. Lam. Positroids, knots, and q,t-Catalan numbers. arXiv:2012.09745

[GL2] P. Galashin, T. Lam. Positroid Catalan numbers. arXiv:2104.05701

[CGGS] R. Casals, E. Gorsky, M. Gorsky, J. Simental. Algebraic weaves and braid varieties. arXiv:2012.06931

[CGGS2] R. Casals, E. Gorsky, M. Gorsky, J. Simental. Positroid links and braid varieties. arXiv:2105.13948

Hilbert schemes of C^2:

[Hai] M. Haiman. Hilbert schemes, polygraphs and the Macdonald positivity conjecture. J. Amer. Math. Soc. 14 (2001), no. 4, 941-1006.

[GNR] E. Gorsky, A. Negut, J. Rasmussen. Flag Hilbert schemes, colored projectors and Khovanov-Rozansky homology. Adv. Math. 378 (2021), 107542, 115 pp.

[OR] A. Oblomkov, L. Rozansky. Knot homology and sheaves on the Hilbert scheme of points on the plane. Selecta Math. (N.S.) 24 (2018), no. 3, 2351-2454.

Links

AIM Research community on link homology

FRG workshop Categorical braid group actions and categorical representation theory.
June 14-18, 2021, University of Massachusetts

Jake Rasmussen's lectures at WARTHOG, 2016.

Problem list from an AIM workshop in 2018
(note: quite a few problems from the list have been solved).

Focused Research Group "Algebra and Geometry Behind Link Homology"