A Quick Overview of my Research- Jesús Antonio De Loera.

I enjoy the interaction between mathematical theory, computation, and its applications. While I consider computational discrete mathematics the core of my research interests, I describe here the many types of mathematics I have done over time. For a more thorough view of my work see this detailed list of all my publications as of June 30th 2022 (in PDF). When I mention number of papers below they refer to numbering in that list of publications.

I started my career in the early 1990's working in the topic of convex & discrete geometry, and computational geometry. My work in the combinatorics and geometry of convex polytopes is now very well-known. In my dissertation, I solved an open question of mathematicians Gelfand, Kapranov and Zelevinsky by finding an example of a non-regular triangulation of the cartesian product of two simplices (se paper [3]). Triangulations appear everywhere, even in the context of Groebner bases of toric ideals. Later I worked very deeply on the problem of finding optimal triangulations and subdivisions of polyhedra. For example in joint work with Below and Richter-Gebert we proved that it is NP-hard to find the smallest triangulation for a 3-dimensional polytope, but I also work on practical ways to find those minimal triangulations for concrete instances (e.g., the minimum triangulation of the dodecahedron has 23 tetrahedra, shown in my main web site) (see papers [1,5,7,9,10,12,13,14]). My first book joint with Joerg Rambau and Francisco Santos Triangulations: Structures for Algorithms and Applications was published by Springer in 2010. It is a thorough reference about triangulations and subdivisions of polyhedra.

I have also published many noteworthy contributions to the problems of computing volumes and integrals of polyhedra (see [30,38,43,49,52,55]), and about counting lattice points (papers [15,17,19,22,23,25,28,45,66]). The list of applications of these computational challenges is very large; from algebraic geometry and representation theory (toric varieties, Gelfand-Tsetlin and Clebsch-Gordan coefficients) to combinatorics (e.g., matroids), computer algebra, and probability and statistics . I have also contributed widely to understanding Ehrhart polynomials and quasi-polynomials in both theory and practice. For example, I have enjoyed looking at their roots and in joint work with Liu and Yoshida we found the first ever closed-form combinatorial formula for the volumes and Ehrhart coefficients of the Birkhoff polytope , i.e., the convex hull of all n by n permutation matrices (see papers [17,19,22,23,24,25,28,31,38,40,49,56,63,71,87]). Our well-known software LattE was started under my direction and initiative, used for research by many mathematicians, and introducing dozens of undergraduates to research. In the current version it can compute Ehrhart quasipolynomials, integrals and volumes.

I continue with enthusiasm my work on understanding the geometry and combinatorics of polytopes (see e.g., papers [21,36,53,66,74,104]). An important family of polytopes are the multi-index transportation problems. These polytopes consist of all real-valued tables, arrays whose entries satisfies given sums from the entries (e.g., row sums, column sums equal to some values). In two indices they are called transportation polytopes and the Birkhoff polytope is an example. Their integer points (called contingency tables by statisticians), and their projections, have been used and appear extensively in the operations research literature due to their importance on scheduling and planning. Their name was coined by Nobel-prize economist T. Koopmans who was interested on the efficient transportation of good by ships.

Back in 1986 several open problems were proposed by Vlach and co-authors. 20 year later, in our paper in SIAM Journal of Optimization (see papers [21,33]), S. Onn and I solved most of them as easy corollaries of the following powerful theorem

Theorem: (De Loera-Onn) Any rational convex polytope and an objective function in the form $\hbox{maximize}\{cy : y\mathbb{R}_{\geq 0}^n, \ Ay=b\}$ is in fact polynomial-time representable as a $3$-way transportation polytope with $2$-marginals $w,v,u$ depending polynomially on the binary size of the input $A,b,c$:

$$\hbox{maximize}\{\,cx:\ \mathbb{R}_{\geq 0}^{r\times c\times 3}\ ... ...j,k}=w_{j ,k}\,,\ \sum_j x_{i,j,k}=v_{i,k}\,,\ \sum_k x_{i,j,k}=u_{i,j}\,\}\ .$$

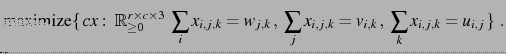
By saying that a polyhedron is representable as another we mean that the polytopes are isomorphic solution spaces are identical and one can transfer one into the other efficiently (in fact a bijection obtained by orthogonal projection to yield the bijection of points). Lattice points transfer to lattice points. The polytopes are combinatorially the same. Thus, one can interpret our theorem as a ``normal form'' or ``canonical reformulation'' algorithm. So, every rational convex polytope can be put in the special form of a multiway transportation polytope for arrays of 3 indices with line sums prescribed. Again, integer solutions get mapped to integer solutions. The consequences for statistical contingency tables are very important too. As a corollary it shows the Markov chains used in Statistical analysis may require arbitrary complex Markov moves for 3-way tables. See papers [21,26,33]. Studying 3-way transportation polytopes is as equivalent to studying all rational polytopes. See our extensive survey in [60].

While I confess polyhedra are my favorite objects in the universe (!!), I also have substantial work in other part of combinatorial geometry and topology. Here are a two examples of my work in this area. Please see my 90 page monograph on applied combinatorial geometry and topology published at the Bulletin of the American Mathematical Society (reference [86]) for more more. First, consider the famous Tverberg's theorem says

Theorem Let a_1,..,a_n be points in d-dimensional Euclidean space. If the number of points n, is sufficiently large, namely n >(d+1)(m-1), then they can be partitioned into m disjoint subsets A_1,...,A_m in such a way that the m convex hulls conv A_1,..., conv A_m intersect.

E.g., for any seven points or more in the plane, one can always color them with three colors such that their convex hulls (smallest convex sets containing the points of the same color) intersect. In topological jargon, Let F = {F_1,.., F_m} be a family of convex sets in Euclidean space. The nerve of F is the simplicial complex with vertex set [m]:={1,2,... , m} whose faces are subsets I contained in [m] such that all the F_i, with i in I, intersect. Thus the classical Tverberg theorem says that, with at least (d+1)(m-1)+1 points, the (m-1)-simplex appears as the nerve of a set m-partition of the points.

One of my lines of work has been to generalize famous theorems from convex geometry to have topological or number theoretic versions (see papers [64,70,72,73,76,77,82,86,93,94,101]). In paper [94] Our main results demonstrated that Tverberg's theorem is but a special case of a much more general situation! For example, we proved that, given sufficiently many points, any tree or cycle, can also be induced by at least one partition of the point set as the nerve of the intersection. We show not all simplicial complexes can be nerves for point set partitions. Together with Tverberg, Helly and Carath\'eodory theorems are the pillars of combinatorial convex geometry. I have proved several notable variations of these classical theorems, in particular some with connections to number theory, topology, and version withcounting lattice points and volume measures as part of the conclusion.

Regarding combinatorial topology, I have been interested in combinatorial questions arising in triangulated manifolds, specially in connection with effective computation. In particular, I was interested in variations of Sperner's lemma about colorings of the vertices of a triangulated ball. The original versions is very important as it is equivalent to the Brouwer's fixed point theorem that is used in game theory and other fields to show the existence of solutions. Most importantly, it is a gateway to computation! The original version is for triangulations of simplices. In our paper [16] we generalized it to triangulations of any convex polytope. A Sperner labelling of the vertices of a triangulation T of a d-dimensional convex polytope P is one where the n vertices of P receive colors 1 through n, and then all vertices of the triangulation T (those new vertices that are not part of the original untriangulated polytope) receive a color, but a vertex inside face F of the polytope P, can only receive a color from the vertices of P inside that face. For example if a face is an edge with colors 3,7, then any vertices of T can only be colored 3 or 7. Here is our theorem:

In other words, following this type of coloring, one always finds a lot of simplices that have different colors in their vertices! At least n-d to be precise. See also my papers [27,51,53,58,59,94,99,101] for more projects with a strong topological content.

Combinatorial Geometry and topology are closely connected to algebraic geometry, geometry of numbers, commutative algebra and representation theory. As a result my research is often concerned with computing with polynomial rings and modules. I am active in the field of Computer Algebra and Symbolic Computing, where I have published many papers (see [4,6,31,37,41,47,52,65,68,100]) where exact symbolic computation with rings is the core of the paper. For example, in [68] My co-authors and I provided efficient randomized algorithms for the problems of (a) solving large (overdetermined) systems of multivariate polynomials equations, (b) finding small, possibly minimal, generating sets of homogeneous ideals. Our approach gives an adaptation of Clarkson's sampling techniques in computational geometry to computations with polynomials. To our knowledge, this is the first time such sampling algorithms are being used in algebraic geometry. Our algorithm relies on being able to compute fast with small-size subsystems, we then sample and solve many small subsystems of the original. We have an iterative sampling scheme where the probability of choosing a polynomial will essentially increase if it was not considered already. In the end, the local information on small subsystems of equations is used to make a global decision about the entire system. The expected runtime is linear in the number of input polynomials and exponential in the number of variables.

Symbolic computation is highly connected to combinatorics. Computers are the laboratory for experimentation and I have done work that uses computers, in particular algebraic algorithms, to investigate graph theory and other combinatorial problems. For example encoding graph coloring questions in terms of ideals of polynomials, rational functions, or lattices and the algebra explains the combinatorics or is used to compute combinatorial information. See [2,37,38,46,47,62,95]

Probabilistic methods have shaped modern combinatorics going back to Erd\"os. Inspired by the study of random graphs, my and co-authors, introduced an Erd\"os-R\'enyi style probabilistic model for monomial ideals and initiated the development of Random Commutative Algebra, aiming to understand the ``average behavior'' of ideals in rings of polynomials. Notably our probabilistic model generalized well-known models on random simplicial complexes (such as those by Kahle, Kalai and Meshulam). In its simplest version, our has parameters $n$, $D$, and $p$, where a random monomial ideal $M$ in $n$ indeterminantes is defined by independently choosing generators of degree $D$, each with probability $p$. We proved theorems about the probability distributions, expectations and thresholds for events involving monomial ideals with given Hilbert function, Krull dimension, and homological information. As it is typical, we think of the probability p as a function of n or D. Here is one concrete nice theorem:

In other words, in our probabilistic model, the equality in the famous Hilbert's syzygy theorem happens to be the most typical situation for non-trivial ideals. I have been working also in various problems on semigroups and toric varieties where we use probabilistic methods for the first time there too (see papers [84,85,88]).

So far I have mentioned mostly ``pure'' math work but my interest in application and computation is very strong! My work is widely recognized as one of the leaders in application of algebra, geometry and topology, in the area of integer and combinatorial optimization. This the part of applied mathematics related to optimizing functions over discrete sets. A famous example of such problem is the traveling salesman problem: Given n cities that must be visited only once, and the costs of going from city i to city j the goal is to find the best order to visit all the given cities in order to minimize the total cost of the trip.

I have been one of the leaders and founders of a new approach to the theory of optimization. In this new point of view, tools from algebra, topology and geometry, that were considered too pure and unrelated to applications, are used to prove unexpected computational or structural results. My second book (joint with Raymond Hemmecke and Matthias Köppe) Algebraic and Geometric Ideas in the theory of Discrete Optimization is the first compilation of results from this novel approach collecting the work of several mathematicians. My award-winning work has provided fundamental new developments taking place in the area of discrete optimization which I summarize here with six significant contributions:

1. Traditionally discrete optimization has focused on how to solve problems with only linear equations or constraints. In pioneering work published in 2006, joint with Hemmecke, Köppe and Weismantel) we proved the first theoretical results for the more difficult model with non-linear objective functions. To put them in context, recall the famous result obtained by H.W. Lenstra Jr. in 1983, states that when the number of variables is fixed and both the objective function $f$ and constraints $g_i$ are linear polynomials, then there is an algorithm to solve it in polynomial time on the input size. Similarly, in another breakthrough, in 2002, L. Khachiyan and L.Porkolab proved that the same holds when the number of variables is fixed and the objective $f$ is a convex polynomial. It is thus a natural question to ask: if we continue to fix the number of variables and the $g_i$ are linear, but the objective function $f$ is an arbitrary non-linear polynomial, what is the computational complexity?

   In a important work we extended the Lenstra's and Khachiyan's results, we answered the question in a paper appeared in journals Mathematics of Operations Research and Math. Programming : We proved that while the problem is NP-hard, even for fixed dimension 2 and degree 4 polynomials, there is a new approximation algorithm to maximize an arbitrary integral polynomial over the lattice points of a convex rational polytope with a fixed dimension. The algorithm produces a sequence of upper and lower bounds for the global optimal value. Surprisingly this is an excellent approximation scheme. The new method codifies the (exponentially many) lattice point solutions, as a short (polynomial-size) multivariate rational generating function (sum of quotients of polynomials) based on the theory put forward by A. Barvinok (we did in LattE the first ever implementation of Barvinok's algorithm). With my graduate students we demonstrated how generating function computations can be used to optimize in practie (all done as part of LaTTE). Later on the theoretical side again, Hemmecke, Köppe and I showed that generating functions provide a similar strong result Lenstra type theorem for integer multiobjective optimization.. Solving multiobjective integer programs with fixed number of variables and fixed number of objective functions can be done in polynomial time or when one has matroid structure. See papers [20,29,30,32,39,44,54].

2. An integer linear program (ILP) is the problem of finding, for given matrix $A$ and vectors $b,c$, the minimum $min \{cx : Ax=b, \ x\geq 0 \ \hbox{integer} \}$. The problem is well-known to be NP-hard; thus one does not expect that a general efficient algorithm can be found. For an ILP $P_b=min \{cx : Ax=b, \ x\geq 0 \ \hbox{integer}\}$ a test set is a finite set of integral vectors such that every feasible non-optimal solution can be improved by adding a vector from the test set. The lattice $L(A)=\{x \in {\mathbb{Z}}^n : Ax=0\}$ has a natural partial order. For $u,v\in {\mathbb{Z}}^n$ we say that $u$ is conformal to $v$, denoted $u\sqsubset v$, if $\vert u_i\vert\leq \vert v_i\vert$ and $u_iv_i\geq 0$ for $i=1,\ldots,n$, that is, $u$ and $v$ lie in the same orthant of ${\mathbb{R}}^n$ and each component of $u$ is bounded by the corresponding component of $v$ in absolute value. The Graver basis of an integer matrix $A$ is the set of conformal-minimal nonzero integer dependencies on $A$. For example, if $A=[1\ 2\ 1]$ then its Graver basis is $\pm \{ [2,-1,0],[0,-1,2],[1,0,-1],[1,-1,1]\}$.

   Graver bases are in fact connected to commutative algebra and algebraic geometry, they are a universal Gröbner bases for the toric ideal associated to the matrix $A$. During the past fifteen years, algebraic geometry and commutative algebra tools have showed exciting potential to solve problems in integer optimization. But, in the past, algebraic methods had always been considered ``guilty'' of bad computational complexity, namely, the notorious bad complexity for computing general Gröbner bases when the number of variables grow. Our research demonstrated that, by carefully using the block structure of matrix $A$, Graver bases can compete (and win!!!) against mainstream tools in integer optimization. Later in paper [67] we showed that one can solve linear optimization (continuous) problems using circuits which is a subset of the Graver basis of a matrix and comes from the circuits of its matroid of linear dependences. We should that the number of steps is polynomial by using steepest circuit increments. Later in paper [102] we continued with this work. The paper that initiated this idea appeared in the journal Discrete Optimization (many more developments have happened in the last years since the publication of paper [34]):

   Fix any pair of integer matrices $A$ and $B$ with the same number of columns, of dimensions $r\times q$ and $s\times q$, respectively. The n-fold matrix of the ordered pair $A,B$ is the following $(s+nr)\times nq$ matrix,

   $$[A,B]^{(n)} \quad:=\quad ({\bf 1}_n\otimes B)\oplus (I_n\otim... ...dots \\ 0 & 0 & 0 & \cdots & A \\ \end{array}\right)\quad .$$

   The number of variables grow, but we can prove

   Theorem Fix any integer matrices $A,B$ of sizes $r\times q$ and $s\times q$, respectively. Then there is a polynomial time algorithm that, given any $n$ and any integer vectors $b$ and $c$, solves the corresponding n-fold integer programming problem.

   $$\min\{cx:\ [A,B]^{(n)}x=b,\ x\in{\mathbb{N}}^{nq}\}\quad.$$

   The key ingredient to make it work comes from commutative algebra. What happens is that for every pair of integer matrices $A\in {\mathbb{Z}}^{r\times q}$ and $B\in {\mathbb{Z}}^{s\times q}$, there exists a constant $g(A,B)$ such that for all $n$, the Graver basis of $[A,B]^{(n)}$ consists of vectors with at most $g(A,B)$ the number nonzero components. This means that it suffices to compute the Graver bases of a small $n$-fold matrix to be able to obtain others. More recently the above theorem has been extended to optimization of convex functions instead of just optimizing linear functions. See paper [35]. Several years later, Graver bases have become a key tool in fixed-parameter complexity results.

3. For applications I have been interested on new methods to solve structured systems of polynomial equations and/or inequalities arising in discrete mathematics and optimization. Recently we worked on on a new technique that reduces non-linear polynomial systems of equations to the solvability of a sequence of large (but sparse) systems of linear equations over finite fields. In 2010 I received the INFORMS computer society award (ICS prize). The ICS Prize is an annual award for best English language paper or group of related papers dealing with the Operations Research/Computer Science interface. INFORMS (The Institute for Operations Research and the Management Sciences) is the largest international organization dedicated to operations research and the science of management. Here is what the prize citation says about the winning papers in combinatorics probability and computing, and in journal of symbolic computation

   ``These two papers introduce a pioneering new approach for proving the optimality of solutions to combinatorial optimization problems. The approach begins by encoding the instance and an objective bound as a system of polynomial equations over a finite field. Then, using Hilbert's Nullstellensatz, the authors demonstrate the effectiveness of a computational method to certify the infeasibility of the polynomial system. The encoding is derived and analyzed for a number of problem classes, such as the k-coloring, stable set, longest cycle, largest planar subgraph, and minimum edge coloring problems. While the degree of the certifying polynomial could be exponentially large, the authors demonstrate that in many cases of interest the degree is low enough to allow for explicit, fast computations. The authors also develop a variety of computational enhancements, including computing over finite fields, exploiting symmetry, adding redundant equations, and applying alternative Nullstellensätze that allow them to solve 3-coloring problems significantly faster than existing methods.

   In this impressive work, the authors take up a mathematical machinery that seemed very unlikely to be useful in practice and turn it into a useful computational algorithm. This work is likely to stimulate additional research into computational polynomial methods, perhaps placing them on the same footing as polyhedral techniques for solving combinatorial optimization problems.'' See papers [41,42,46,47]

4. I have considered many other structured problems in optimization both continuous and discrete. With my co-authors I considered the problem finding the minimal number of linear of constraints that define a problem with exactly k integer solutions. In [61,64,66] we proved a generalization of Bell-Scarf-Doignon theorem that gives a bound. Much work has followed since inspired by our paper! Another structural problem is the \emph{sparsity of solutions} for the integer optimization problems max {c^T x : Ax =b, x>= 0, x \in Z^n}, where A is an m by n integer matrix, b is an integer m-vector and c an integer n objective function vector. % For a solution vector x, its support is the number of non-zero entries. In our papers we established lower and upper bounds on the \emph{minimal size of the support of an optimal solution} of an integer optimization problem. Similar problems were studied by E. Candes and T. Tao over real variables resulting on the famous compressed sensing techniques. Our intention was to investigate the discrete version. Our bounds are polynomial in the number of inequalities m and the largest binary encoding length of an entry of the matrix A and they are independent of the objective function. Bounds on the support are applicable in applied optimization. E.g., minimal support estimates were an ingredient in the best algorithms to solve several instances of the cutting-stock problem: this is the practical challenge to cut pieces of stock material, say fabric rolls, paper rolls or sheet metal, into smaller pieces of specified sizes, while minimizing the material wasted. See papers [78,83,92,96].

   Another noteworthy contribution during this period is my work on stochastic optimization (see paper [79]). Chance-constrained optimization is a branch of stochastic optimization which concerns problems in which constraints are imprecisely known, but the problems need to be solved with a minimum probability of reliability or certainty. Such problems arise naturally in many areas of finance (e.g., investment portfolio planning where losses should not exceed some risk threshold), in telecommunication (services agreements where contracts require network providers to guarantee with high probability that packet losses will not exceed a certain percentage), and in the planning of medical emergency response services (where one wishes to have high probability of coverage, overall possible emergency scenarios). My co-authors and I provided a new algorithm, for when the problems have decision variables (yes/no decisions have to be taken). Chance-constrained problems are notoriously difficult to solve because the region of possible solutions is often not convex and because the probabilities of events can be hard to compute exactly. Our sampling algorithm reduces the original stochastic problem to solving several deterministic convex mixed-integer programming problems. How many? The performance of the algorithm depends on the number of samples, and this depends linearly on the number of continuous variables and exponentially in the number of discrete variables present. The more yes/no decisions one needs to make in a process, the more expensive it will be to approximate. Sampling techniques are essential in large-scale linear optimization computation when we cannot even read the entire system (see [45]).

5. Linear optimization problems (optimizing linear function over linear conditions) are crucial as they are subroutines in more difficult optimization problems. Fields medalist Steven Smale listed the problem of finding a strongly polynomial algorithm for linear optimization, possibly via a polynomial version of the simplex method, as one of the key mathematical problems in the 21st century. I agree! Thus I have worked in the study of linear optimization algorithms with gusto! In paper [48,89] I surveyed the complexity and geometry of various linear optimization algorithms. I am proud to say that what I described below was in big part the reason for me to win the 2020 INFORMS Farkas prize and being selected SIAM fellow in 2019:

   First, in paper [50] we studied geometry of interior point methods. The central path is the key object in interior point methods algorithms and software. In joint work with Vinzant and Sturmfels (paper published in Foundations of Computational Math, we gave exact algebraic formulas for the central path, determined the degree, and genus of the curve. These invariants, along with the degree of the Gauss image of the curve, are expressed in terms of a matroid of the input data. As an application we give an instance-specific bound of the total curvature of the central path, a quantity relevant for the performance of interior point methods. The key mathematical ``liaison'' we managed to established is that the differential geometry of a central curve is intimately connected to that of the underlying matroid of the constraints. I am very proud this paper later led to the work by Allamigeon, Benchimol, Gaubert, Joswig, showing that the curvature can be exponential. This had big consequence for interior point algorithms.

   I have also made significant contributions regarding the geometry of the famous simplex method. The simplex method, uses the fact the region of possible solutions is a polyhedron and, starting at an initial vertex, it traces a path on the graph of the polyhedron until it finds an optimum. SIAM selected the simplex method in 2000 as one of the top 10 most influential algorithms in the 20th century due to its practical and theoretical influence. First, the problem of bounding the number of iterations of the Simplex algorithm motivates bounding diameters of graphs of simplicial complexes. Billera and Provan had proposed in 1979 a conjecture that if true would have proved a linear bound to the diameter of all polyhedra, namely twice the number of facet defining inequalities. The idea relies on a clever decomposition of simplicial complexes by a sequence of removals of lower dimensional faces. In paper [53] paper published in Mathematics of Operation Research in 2012 (joint work with former postdoc Steve Klee), we solved their open question about their method to bound the diameter of convex polyhedra on the negative. We disproved the conjecture showing that the conjecture fails in a 4-dimensional example coming from transportation optimization problems. The construction is very elegant and uses topological tools (e.g., shellability, simplicial complexes contractions, deletion and other operations of edges).

   Again the problem of bounding the number of iterations of the Simplex algorithm also motivated my papers [98,102]. This time the setup is not topological we investigated the possible lengths of monotone paths followed by the Simplex method inside the oriented graphs of inequality-defined polyhedra (oriented by the function we optimize). We considered bounds for the shortest and the longest monotone paths. Our bounds are applicable in many situations. In contrast, we proved that computing a shortest (monotone) path to an optimal solution on the 1-skeleton of a polytope is NP-hard, and it is even NP-hard to approximate within a factor better than 2. Studying the simplex method in special families of polyhedra can have important consequences. In a major breakthrough, former postdocs Borgwardt, Finhold, and I showed in [69,80] the graph diameter of a network-flow polytope, for a network with $n$ nodes and $m$ arcs is never more than $m+n-1$. This was a significant result because this bound is not true for general problems and network-flow problems are of great importance in Computer Science and Operations Research. An exciting mathematical result is that the set of monotone paths of a linear program has a nice topological structure, a polyhedral complex homotopic to a ball. It is called \emph{monotone path complex (or Baues complex}. Its vertices are precisely all the possible monotone paths on the linear program. This follows from the work of Billera-Kapranov-Sturmfels on fiber polytopes. In paper [97] (with Athanasiadis and Zhang) we looked at the 1-dimensional skeleton of this the topological structure and find extreme values for the number of vertices of this and their diameter in terms of the input data of the linear program. Second, the performance of the simplex method depends on a \emph{pivot rule} that decides which path to follow in the graph search. A pivot rule chooses how to trace the path to the optimal solution. It is a famous open question whether there is a pivot rule that can always choose a polynomial-length path. Trying to approach this important problem in [106] my co-authors and I constructed a ``moduli space of pivot rules'' based on prior Fiber polytope constructions and [97]. For this purpose we identified that among all pivot rules the \emph{normalized-weight pivot rules} are fundamental for the following reasons: First, their pivots are governed only by local information and the union of all paths traced form an arborescence. Second, many of the most used pivot rules are NW pivot rules, and third, we show this subclass is critical for understanding the complexity of all pivot rules as they have the shortest paths of all pivot rules. Thus if there is a efficient pivot rule, there will be one that is an NW pivot rule. Our main theorem is that the normalized-weight pivot rules can be parametrized in a natural continuous manner and show there exists a \emph{pivot rule polytope}, whose vertices are in bijection with all normalized-weight pivot rules of a linear program. We explain their face structure and compute upper bounds on the number of vertices of our pivot rule polytopes. Regarding special families we presented in [102,105] new pivot rules for the Simplex method for LPs over 0/1 polytopes where the number of non-degenerate steps taken using these rules is strongly polynomial and even linear in the dimension or in the number of variables. Our bounds on the number of steps are asymptotically optimal on several well-known combinatorial polytopes. Our analysis is based on the geometry of 0/1 polytopes and novel modifications to the classical Steepest-Edge and Shadow-Vertex pivot rules.

I have always been fascinated by the beautiful geometry behind statistics and data science questions (see e.g., my earlier work in algebraic methods for Markov chains and statistical models analysis (see e.g., [18,21,26]). Now I am excited to report that since 2018 I started to work more seriously on the foundations of Machine Learning and Statistical Inference. This is a fast developing area with opportunities for mathematicians.

My most recent work contains several powerful situations where famous theorems in discrete geometry answered natural questions from machine learning and statistical inference. For instance in my paper [93] we showed the problem of deciding the existence of Maximum likelihood estimator in multiclass logistic regression, is equivalent to stochastic versions of Tverberg's theorem in combinatorial geometry. We presented bounds on the probability that m random data of colored classes all contain a point in common in their convex hulls (points are colored at random). We also discuss connections to condition numbers for analysis of steepest descent algorithms in logistic regression. See papers [93,101]. There is even more beautiful polyhedral geometry in studying reinforcement learning algorithms (see [103]) and in algorithms of quadratic programming that are used in feature recognition (see [81,91]). Finally, in the more pragmatic and experimental paper [90] we asked, can machine learning algorithms lead to more effective outcomes for optimization problems? We trained machine learning methods to automatically improve the performance of optimization and signal processing algorithms. We used our approach to improve two popular data processing subroutines in data science: stochastic gradient descent and greedy methods in compressed sensing. We provide experimental results that show machine learning algorithms do lead to more effective outcomes for optimization problems helping us tune the algorithms. Stay tuned for more work!